В школе часто задают задачку: рассчитать глубину колодца, если в наличии есть только камень и секундомер. При этом предлагается воспользоваться простейшей формулой для измерения координаты тела, падающего равноускоренно без нулевой скорости: \[ h = \frac{gt^2}{2}, \]
где \(h\) — путь (глубина колодца), \(g\) — ускорение свободного падения, \(t\) — время на секундомере.
При этом упускается важнейшая деталь. Скорость звука на этой планете очень невысока. Естественно, как только камень по параболе упадёт на дно, звук со дна начнёт лететь равномерно и прямолинейно, безо всякого замедления. Ушей слушателя он достигнет через время, равно отношению глубины ущелья к скорости звука. Если глубина невелика, то тогда всё нормально. Однако при глубине в 123 метра (или высоте, что то же самое; 123 метра — это высота 33-этажного MCI Centre в Лос-Анджелесе... или любого другого здания подобной этажности) звуку потребуется более трети секунды, чтобы достичь ушей слушателя. Как видно из иллюстраций, дальше — больше. Расстояние квадратично зависит от времени, поэтому доля возврата звука обратно в общем измеренном времени неуклонно растёт.
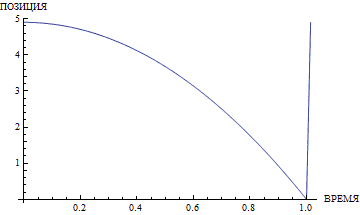
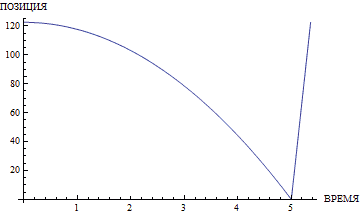
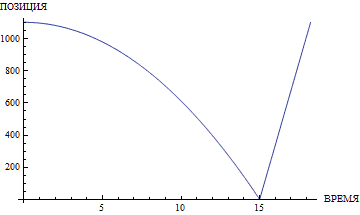
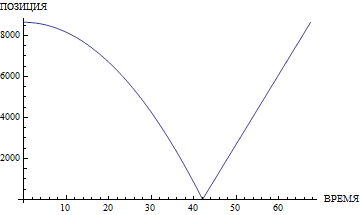
Если бы мы в модели с конечной скоростью звука просверлили в центре Эвереста отверстие-тоннель до земли и бросили туда камень, то он бы падал примерно 42 секунды, а обратно звук бы дошёл за половину этого времени (!). Радостные, мы бы стояли с секундомером, получили бы примерно минуту, подставили бы её в формулу \(h = \frac{gt^2}{2}\) и вычислили бы высоту Эвереста, которая бы отличалась от истинной в бо́льшую сторону... всего в несколько раз (иными словами, мы бы определили высоту горы с точностью до константы).
В формуле расчёта расстояния требуется ввести корректировку на скорость звука. Если этого не сделать, с каждой следующей секундой относительная погрешность измерения будет увеличиваться на 1,8–2 процентных пункта. Поэтому скорректируем наш ответ с учётом знания того, что скорость звука конечна и равна некой \(c\).
Звук летит равномерно прямолинейно без ускорения. Человек с секундомером измеряет сумму двух временных промежутков: время полёта камня (\(t_1\)) и время возврата звука (\(t_2\)). То есть мы знаем \(t = t_1+t_2\), а в формулу высоты, с которой падает тело, надо подставлять \(t=t_1\): \(h = \frac{gt_1^2}{2}\). Более того, \(h = \frac{gt_1^2}{2} = ct_2\), \(t=t_1+t_2\). Выразим \(t_1\) через \(t\): \[ h = \frac{gt^2_1}{2} = ct_2 \quad \leadsto \quad t_2 = \frac{gt_1^2}{2c} \] \[t = t_1 + \frac{gt_1^2}{2c} \quad \leadsto \quad \frac{g}{2c}t_1^2 + t_1 - t = 0\] \[D = b^2-4ac = 1 + \frac{2gt}{c} \quad \leadsto \quad t_1 = \frac{c}{g}\left( \sqrt{1 + \frac{2gt}{c}} -1 \right)\]
Скорость звука (о ней будет сказано ниже) нам известна (≈340 м/с), ускорение свободного падения тоже известно (9,80665 м/с²). Поэтому итоговая формула, позволяющая определить высоту объекта по времени падения камня, который стучит о дно, будет иметь вид: \[ h = \frac{gt_1^2}{2} = \frac{c^2}{2g}\left( \sqrt{1 + \frac{2gt}{c}} -1 \right)^2 = c\left( t - \frac{c}{g} \left( \sqrt{1 + \frac{2gt}{c}} +1 \right) \right).\]
Легко убедиться в том, что при очень большой скорости звука время \(t_1\) будет стремиться ко времени \(t\): \[ \lim\limits_{c\rightarrow\infty} \frac{c}{g}\left( \sqrt{1 + \frac{2gt}{c}} -1 \right) = \lim\limits_{c\rightarrow\infty} \frac{c}{g}\frac{\left( \sqrt{1 + \frac{2gt}{c}} -1 \right)\left( \sqrt{1 + \frac{2gt}{c}} +1 \right)}{\left( \sqrt{1 + \frac{2gt}{c}} +1 \right)} = \] \[= \lim\limits_{c\rightarrow\infty} \frac{c}{g}\frac{2gt}{c\left( \sqrt{1 + \frac{2gt}{c}} +1 \right)} = \lim\limits_{c\rightarrow\infty} \frac{2t}{ \sqrt{1 + \left\{\frac{2gt}{c_{\rightarrow\infty}} \right\}}_{\rightarrow0} +1 } = \lim\limits_{c\rightarrow\infty} \frac{2t}{\sqrt1 + 1} = t.\]
Вашему вниманию предлагаются графики, демонстрирующие отклонение результатов подсчёта по «школьной» и по скорректированной формуле.
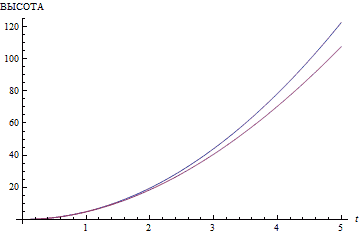
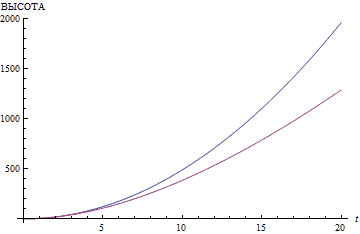
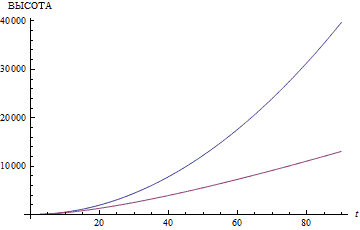
Всем хороша данная модель, только сопротивления воздуха она не учитывает. Во второй части данной статьи я введу более совершенную модель, в которой будет учтена температура воздуха, его плотность, а также масса и аэродинамические свойства падающего объекта.