Иллюстрация парадокса Симпсона: если в генеральной совокупности отсутствует взаимосвязь, то может найтись способ создать произвольную версию при дроблении по выборки по некоторому эндогенному механизму. Иногда это называется эндогенной стратификацией: вероятность отбора наблюдения в выборку даже при условии всех экзогенных переменных не независима от значений, принимаемых зависимой переменной или эндогенным включённым регрессором.
Предположим, изначально у нас было одно полное облако точек. Мы разделили его на три непересекающихся подмножества (обозначены цветами). В каждом из цветных облаков есть значимая взаимосвязь между переменными \(X\) и \(Y\), которую обнаруживают любые регрессионные методы (приведены три: классический МНК, квантильная регрессия при \(q=0{,}5\) и локально линейная регрессия первой степени).
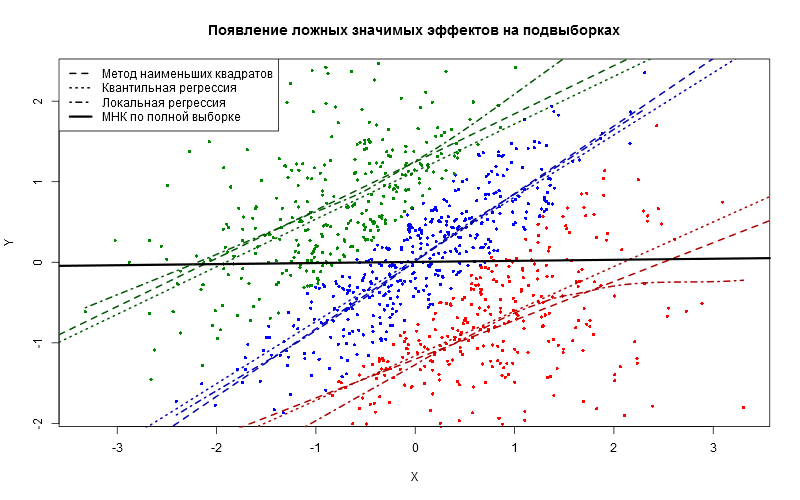
Однако если взглянуть на изначальное облако из всех точек всех трёх цветов, то эффекта никакого не будет (эта ничтожно слабая и малозначимая зависимость показана толстой чёрной линией). Получается парадокс: если индивид относится к зелёной подвыборке, то в ней влияние \(X\) на \(Y\) есть. То же верно и для всех остальных подвыборок. Везде эффект положительный! Однако одновременно для всех точек никакого эффекта нет.
| Вся выборка | Синие | Зелёные | Красные | |
|---|---|---|---|---|
| Зависимая переменная: Y | ||||
| X | 0.013 | 0.839*** | 0.482*** | 0.598*** |
| Стд. ошиб. X | (0.030) | (0.024) | (0.048) | (0.046) |
| t-стат. X | 0.431 | 35.6*** | 7.7*** | 13.6*** |
| Константа | 0.004 | 0.013 | −1.202*** | 1.245*** |
| Стд. ошиб. конст. | (0.031) | (0.019) | (0.055) | (0.053) |
| Наблюдений | 1000 | 386 | 307 | 307 |
| R2 | 0.0002 | 0.756 | 0.252 | 0.361 |
| Стд. ошиб. остат. | 0.981 | 0.373 | 0.667 | 0.640 |
| Примечание: *p<0.1, **p<0.05, ***p<0.01 |
В скобках приведены робастные стандартные ошибки в форме Дэвидсона—Маккиннона (HC3).
Вывод: чем более избирательно исследователь будет составлять выборку для исследования («пожилое коренное население, которое до этого трудилось на работах, не требующих высокой квалификации»), тем больше вероятность, что он что-нибудь да обнаружит... и что эта находка будет ложной.
Код для репликации в R:
library(lmtest)
library(sandwich)
n <- 1000
set.seed(100)
x <- rnorm(n)
y <- rnorm(n)
th <- 0.7
g1 <- (y < x + th) & (y > x - th)
g2 <- (y <= x - th)
g3 <- (y >= x + th)
coeftest(lm(y~x), vcov. = vcovHC)
coeftest(lm(y~x, subset=g1), vcov. = vcovHC)
coeftest(lm(y~x, subset=g2), vcov. = vcovHC)
coeftest(lm(y~x, subset=g3), vcov. = vcovHC)