«Репрезентативная выборка» — запутывающее студентов определение

В науке выстроенные вокруг заблуждений теории или вшивые методы выходят из употребления не потому, что кто-то показывает их несостоятельность или публикует в престижном рецензируемом журнале статью с критикой, опровержением или предложением менее вшивой методологии; они отмирают тогда, когда умирают использующие их исследователи и когда следующее поколение подхватывает методы, которые лучше работают на практике, проходят проверку на адекватность и на робастность, а главное — (пока) не вызывают критики со стороны тех, кто умеет отсеивать старую дрянь. Увы, зачастую старый бред лучше проиндексирован в поиске и процитирован массой прикладных исследователей, применяющих методы без понимания их ограничений, поэтому количественные признаки авторитетности старых учебников прирастают чисто технически. Пример того, как с этим феноменом можно и нужно бороться, — это история феномена квазимультиколлинеарности.

Ещё в 1991 г. Артур Голдбергер в своём легендарном учебнике «A course in econometrics» порадовал читателя донельзя потешным пассажем о том, как бы выглядела глава о выборочном среднем, если бы проблемы расчёта среднего на малых выборках рассматривались в том же ключе, что и проблемы оценивания линейной регрессии с небольшим числом наблюдений. В главе 23, «Мультиколлинеарность», он вводит шуточное определение «микронумеричность» («micronumerosity»), а затем очень тонко издевается над теми, кто не понял юмора, в заголовке раздела 23.4 «Когда мультиколлинеарность желательна». Профессор Дэвид Джайлс в своей публикации 2011 г. отмечает, что качество учебника по эконометрике обратно пропорционально тому, сколько страниц уделяется (квази-)мультиколлинеарности. К счастью, новые учебники стараются уделять меньше страниц этой мешанине, акцентируя внимание на том, что это наложение проблемы спецификации модели (которую можно решить переспецификацией) и проблемы недостаточного числа наблюдений (которую нельзя решить). Традиционные методы (как правило, те, где имеет значение численная обусловленность матриц при обращении и где любая неточность умножается на число обусловленности, conditioning number) чувствительны к этой проблеме, но более новые альтернативы могут запросто съесть матрицу с линейно зависимыми столбцами и не поперхнуться. В частности, в градиентном бустинге и регрессионных деревьях поиск точки разделения происходит линейно по упорядоченным значениям всех переменных.

Пока мы ждём момента, когда выйдут на нулевой уровень потребления кислорода те, кто с невозмутимым видом делает утверждения вида «квазимультиколлинеарность — это серьёзная проблема, которая убивает исследование», к сожалению, до сих пор — в 2024 году! — ещё работают преподаватели — причём некоторые из них в престижных университетах, — которые на самой первой лекции по математической статистике понятие выборки определяют через некую «репрезентативность». Это прискорбно, и ниже предлагается объяснение, что такое выборка, почему «репрезентативность» — это такая же неоднозначная мешанина свойств, как и «квазимультиколлинеарность», и почему этого слова в определении быть не должно.

Широкое и узкое определение выборки

В самом широком (гуманитарном) смысле статистическая выборка — это набор независимых реализаций (т. е. исходов) из одного и того же распределения случайных величин. Это то, что можно получить, имея закон (причём обычно нам неизвестный) многомерного распределения, проистекающего из некоторого эфемерного «повторяемого эксперимента природы». В этих исходах нигде не появляется никакая «репрезентативность»; всё, что даёт истинное многомерное распределение при каждом следующем случайном эксперименте, — всё есть выборка.

Случайные (рандомизированные) эксперименты — это эталонный способ получения данных для оценивания каузальных эффектов и причинно-следственных связей. Во-первых, оценки эффектов на подобных данных являются несмещёнными, коль скоро спецификация используемой модели верна или, если ослабить требования, хотя бы выполняются условия первого порядка, обеспечивающие идентификацию параметров. Во-вторых, в среднем исчезает эффект вмешивающихся факторов, искажающих результаты (confounding factor), так как при выполнении вышеупомянутых условий случайный шум усредняется в константу.

Пример. Если случайный эксперимент — соединение родительских хромосом, то единица наблюдения — человеческое существо, а многомерная случайная величина — вектор физических характеристик индивида. Природа подбрасывает монетку, и мы рождаемся мужчиной с голубыми глазами, ростом 177 см и родинками на правой (но не на левой) руке. Подбрасывает монетку ещё раз — и рождается ещё несколько миллиардов человек.

В узком (формальном) смысле слова выборка — это многомерная случайная величина, состоящая из n независимых и одинаково распределённых случайных величин. В этом определении фигурирует размер выборки — n. Предположим, что в кабинете есть 20 столов, за каждый из которых можно усадить одного респондента, чтобы спросить у него вес, рост, возраст (и всё прочее, что нужно для «Тиндера») — скажем, 30 переменных. Сегодня мы запускаем 20 человек и собираем информацию об их тридцати социоэкономических характеристиках. Завтра мы запускаем 20 человек и тоже собираем информацию об их тридцати социоэкономических характеристиках. Каждый день мы получаем 20 реализаций случайного эксперимента, каждая из которых представляет собой 30-мерную случайную величину, и это называется выборкой размера \(n=20\).

Отличительная особенность случайной выборки состоит в том, что знание \(n=20\) наборов характеристик не даёт никакой возможности предугадать, какими будут значения у всех последующих респондентов. Каждое новое наблюдение в выборке, которое вот-вот зайдёт в кабинет — это сюрприз; тем не менее, старые наблюдения сюрпризом не являются, так как в них нет неопределённости. Строчка базы данных, в которой записаны наблюдённые у индивида 30 значений, — это исход; как только появляется новая реализация и становятся известны 30 численных значений, это перестаёт быть случайной величиной. В понедельник вечером «ответ 13-го респондента во вторник» — это случайная величина; во вторник вечером это исход эксперимента.

Определение выборки, в которое запаяно количество наблюдений n, часто используется в областях статистики, где «размер имеет значение», а статистические свойства оценок зависят от n. К примеру, если наблюдений мало и на центральную предельную теорему (ЦПТ) нет никакой надежды, то исследователи от отчаяния начинают ругаться словами вроде «вложенный бутстрап» и скрупулёзно изучать причины, по которым они не имеют морального права применять простые старинные асимптотические формулы, которые вшиты во все статистические пакеты. В этих изысканиях проскакивает словосочетание «выборочное распределение», компьютер для получения каких-либо результатов приходится оставлять включённым на ночь, а в это время исследователь спит и во сне гуляет по параллельным вселенным и собирает в них данные повторных экспериментов на разных выборках. С другой стороны, в большинстве приложений — особенно бакалаврских! — не имеет значения, набрано в выборку 100 или 1000 наблюдений, так как всегда за выборкой стоит одна и та же генеральная совокупность с одним и тем же совместным распределением случайных величин и одними и теми же закономерностями между ними: таково определение выборки...

Проблемы со случайными выборками многомерных случайных величин

Как бы нам ни импонировала идея уподобляться всяческим слепым богиням и набирать наблюдения в выборку случайным образом, использование в практических целях случайного набора наблюдений из генеральной совокупности не гарантирует сбалансированности данной выборки в плане схожести эмпирического распределения некоторых величин с теоретическим. Асимптотически, конечно, сходимость эмпирической функции распределения вероятности к теоретической будет достигнута, но бюджеты асимптотическими не бывают, поэтому приходится думать: если собрать у 2000 респондентов ответы на 100 вопросов, то какой процент из них будет похож на распределение ответов в генеральной совокупности? В случайных выборках очень часто не только многомерные, но даже одномерные распределения некоторых случайных величин могут сильно отличаться от истины, и причина одна: просто не получилось, так легли карты, так выпали кости, так у бабушки из романа Достоевского «Игрок» выпадал zéro.

Чем больше переменных — размерность случайной величины, — тем выше шанс получить выборочное среднее, выборочные квантили и прочие описательные статистики хотя бы одной переменной, не похожие на их истинные популяционные значения. Эта проблема сродни проблеме ложноположительных результатов и ошибок первого рода: если вероятность ошибочно отвергнуть верную нулевую гипотезу равна 5%, то вероятность отвергнуть её хотя бы один раз после проведения этого теста 10 раз на разных выборках равна \(1 - (1-0{,}05)^{10} \approx 40\%\). Чем больше показателей мы измеряем, тем выше вероятность, что хотя бы один из них будет иметь в выборке среднее, значимо отличающееся от истинного математического ожидания.

В экономике очень часто собирается один набор данных для ответа на один исследовательский вопрос, в котором у каких-то переменных распределения похожи на популяционные, а у каких-то — не похожи. Пример — панельные наборы данных (РМЭЗ, ECHP, PSID), в которых опросники содержат десятки страниц, на которых фигурируют такие вопросы, как «сколько килограммов яблок вы собрали на участке». Достоверное оценивание совместных распределений десятков случайных переменных в данном случае безнадёжно. Кроме того, респонденты устают, не могут или не хотят дать ответ на какой-то вопрос, из-за чего часть наблюдений для некоторых переменных может быть пропущенной. При наличии пропусков в наблюдениях невозможно описательными статистиками этих переменных по доступным данным оценить их популяционные аналоги, не зная механизма пропажи наблюдений или не делая дополнительных предположений.

Проблема конечности выборок («\(n\to \infty\), но \(n < \infty\)») также порождает так называемое «проклятие размерности»: чем больше переменных, тем больше разрастается размерность многомерного облака наблюдений, и поэтому почти все наблюдения лежат на границе выпуклой оболочки данных. Это затрудняет применение многих параметрических и непараметрических методов, используемых для оценивания условных математических ожиданий и тестирования гипотез о функционалах распределений. Даже в обыкновенной линейной регрессии и методе моментов после записи «\(n \to \infty\)» оговаривается, что если в модели используется \(k\) регрессоров, то накладываются ограничения и на \(n/k\), то есть на соотношение числа наблюдений и числа параметров модели (как правило, \(n/k \to \infty\), хотя есть и другие альтернативы). Старожилы иногда шамкают: «Количество наблюдений должно превышать количество регрессоров хотя бы в четыре раза». Медсёстры дома престарелых им отвечают: «Что вы, дедушка, всё зависит от того, какой момент оценивается: оценки средних у распределений без тяжёлых хвостов и при \(n=20\) надёжны, а на оценки коэффициента эксцесса и при \(n=200\) лучше не дышать, так как там четвёртая степень фигурирует — помилуйте, какие четыре раза, вот вам утренняя доза донепезила...»

Стратифицированные выборки

Особенно опасно полагаться на случайные (рандомизированные) выборки и надеяться на отсутствие значимых различий между выборочными и популяционными средними при оценивании эффекта воздействия в медицине. Ещё в 1930-е годы Госсет (Стьюдент) и Йейтс предлагали закладывать сбалансированность показателей при составлении выборки в ущерб случайности отбора. Неслучайные механизмы отбора выборки могут повысить точность результатов, однако их трудно реализовать на практике.

Самый популярный способ сбора данных под флагом этой самой «рЕпрЕЗенТАтИвНОстИ» — это стратифицированная выборка. Пространство нескольких (всех не получится) характеристик делится на непересекающиеся области \(A_1, \ldots, A_k\), и исследователь набирает \(n_1, \ldots, n_k\) наблюдений из каждой области. Например, принимается решение опросить 100 человек мужескаго полу от 20 до 29 лет, 156 мужчин 30–39 лет и 138 мужчин 40–49 лет, а также столько же женщин в каждой возрастной категории, так как при этом соотношения человек в группах будут напоминать соотношения из половозрастной пирамиды по официальным данным.

Помимо баланса по нескольким ключевым показателям, стратифицированная выборка может обеспечивать более точные оценки выборочных средних. Кроме того, если заранее обрисовать задачу «опросить по 100 мужчин и по 100 женщин из Парижа и из Берлина», то тогда легче организовывать поездки анкетёров и проверять, достигнута ли заложенная в выборку пропорция переменной пола. Собранная таким образом стратифицированная выборка будет хотя бы по нескольким переменным гарантированно походить на теоретическое совместное распределение этих избранных переменных, но при этом она не будет случайной!

Более того, при наличии любой выборки невозможно без информации о теоретических характеристиках определить, стратифицированная она или нет. Не всякая стратифицированная выборка имеет совместное (или хотя бы даже индивидуальное) распределение переменных, как в генеральной совокупности. Некоторые стратифицированные выборки содержат непропорционально больше наблюдений из некоторых групп (например матери-одиночки с детьми, чтобы мочь хоть как-то по их данным понять их проблемы и сформировать меры поддержки), и этот дисбаланс можно диагностировать только при наличии информации о генеральной совокупности или о протоколе сбора информации! Информация о когортах должна обязательно поступать от того, кто планировал сбор данных, тому, кто эти данные использует. Несмотря на это, некоторые исследователи могут использовать «стратифицированную выборку» без проверки характеристик переменных; даже если в базе данных даются стратификационные веса, то и опытный исследователь не сразу сообразит, умножать на них надо или делить.

Даже если есть сведения о средних значениях популяции, для достижения сходства с ними выборочных показателей опасно пытаться балансировать выборку отдельно по каждой переменной, так как при этом искажается совместное распределение переменных. Если для того, чтобы сблизить средние значения или пропорции в популяции и в выборке, подтачивать и отбрасывать крайние наблюдения, особенно когда существенная часть наблюдений лежит на границе выпуклой оболочки в многомерном пространстве признаков, то это «сдует» всю выпуклую оболочку во всех измерениях и искусственно занизит вариабельность данных, а также отрежет края распределений и сделает невозможным анализ зависимости хвостов, оценивание копул и проч.

Следовательно, не стоит радоваться, даже если написано, что выборка сбалансирована по такой-то и такой-то переменной; вероятность того, что выборочные характеристики будут отличаться от параметров генеральной совокупности, по-прежнему очень высока.

Оценивание моделей на непрезентативных выборках

Даже несбалансированные выборки, не похожие на генеральную совокупность, могут прекрасно использоваться в анализе и давать безо всякой коррекции состоятельные оценки, верные для генеральной совокупности. Если на вероятность отбора наблюдения в выборку влияет переменная интереса (зависимая переменная) или эндогенная переменная, то подобный механизм отбора называется эндогенным, а если влияет экзогенная переменная (или совокупность исключительно экзогенных переменных), то экзогенным.

Конечно, если рассчитываются выборочные характеристики переменных (дескриптивные статистики), то состоятельные оценки среднего, дисперсии и проч. есть шанс получить без дополнительных премудрствований только тогда, когда соотношения количества наблюдений во всех стратах совпадают с соотношениями вероятностей попасть в регионы разбиения у истинного распределения — иными словами, когда выборка случайная или когда удалось простратифицировать выборку по всем переменным и набрать нужное число наблюдений во все страты (обычно это бывает во сне). С другой стороны, есть масса случаев, когда стратификация (или отсутствие оной) не имеет ровным счётом никакого значения или перестаёт его иметь после применения примитивного взвешивания.

Предположим, оценивается некоторая линейная регрессионная модель:

\[ Y = \alpha + X'\beta + U, \quad \mathbb{E}(U\mid X) = 0,\]

где \(Y\) — зависимая переменная, \(X\) — экзогенная объясняющая переменная (включённый инструмент).

Если механизм отбора из генеральной совокупности в выборку экзогенный — то есть если значения экзогенных переменных влияют на вероятность попасть в выборку \(p(X)\) — то тогда этот механизм можно легко проигнорировать, это не скажется на состоятельности оценок коэффициентов наклона \(\beta\). Его также можно учесть, используя \(1/p(X_i)\) в качестве весов наблюдений, но это отразится только на асимптотической дисперсии оценки; предел по вероятности точечной оценки останется тем же.
Пример: в выборку попало вдвое больше женщин из возрастной категории 30–39 по сравнению с остальными стратами; так как пол и возраст всегда экзогенные, то стратификация экзогенная.
Даже с эндогенной стратификацией при наличии информации о механизме отбора \(p(Y, X)\), если этот механизм обратимый (\(p(Y, X) \ne 0\)), можно состоятельно оценить параметры модели, используя \(1/p(Y, X)\) в качестве весов.
Пример: после опроса некоторого количества индивидов было посчитано количество индивидов с заработной платой свыше 1000 €, и затем было опрошено ещё столько же людей с заработной платой свыше 1000 €.

Более того, урезание / фильтрация выборки по значениям объясняющих переменных как экстремальная форма экзогенной стратификации не сказывается на состоятельности оценок параметров моделей. Удаление наблюдений из выборки на основе фильтра по значениям экзогенных переменных \(X\) приведёт лишь к искажению выборочных средних и несостоятельности \(\bar X_n\) для оценки \(\mathbb{E}X\), но оценка каузального эффекта \(\hat\beta\) в структурной модели останется несмещённой!

Пример с доказательством. Предположим, \(X\) — возраст работающего индивида (средний возраст — 42 года). Для оценивания зарплатного уравнения Минцера, где \(Y\) — зарплата, выборка урезается только до набора \(X < 30\), и в ней средний возраст становится 24 года. Оценка эффекта возраста при добавлении ограничения на выборку «возраст меньше 30» не теряет состоятельности, так как оценивается изменённая модель, где все переменные умножены на индикатор \(\mathbb{I}(X < 30)\):

\[ Y\cdot \mathbb{I}(X < 30) = \alpha \cdot \mathbb{I}(X < 30) + [X \cdot \mathbb{I}(X < 30)]'\beta + U\cdot \mathbb{I}(X < 30),\]

а исходное предположение валидности спецификации модели \(\mathbb{E}(U\mid X) = 0\) по-прежнему верно. Состоятельность МНК зависит от того, экзогенен ли новый регрессор \(X \mathbb{I}(X < 30)\) по отношению к новой ошибке \(U \mathbb{I}(X < 30)\). Это легко доказать, так как \(\mathbb{E}(U \mid X) = 0 \Rightarrow \mathbb{E} [f(X)U] = 0\) для любой функции \(f(X)\). В данном случае \(f(X) := \mathbb{I}(X < 30)\), а \(f^2(X) = f(X)\). Тогда

\[ \mathbb{E} (U \mid X) = 0 \rightarrow \mathbb{E}[X f(X) U f(X)] = 0,\]

а это и есть условие первого порядка, дающее МНК-оценку при ограничении «возраст меньше 30».

Следовательно, ограничение выборки по экзогенному показателю не может пошатнуть состоятельность оценок моделей.

С урезанием выборки по эндогенным переменным такой фокус не пройдёт (возникнет смещение отбора, как в моделях Тобина и Хекмана), однако использование механизма отбора наблюдений, где для каждого наблюдения вероятность отбора ненулевая (хоть и произвольным образом зависящая от значений эндогенной переменной), оправданно, если исследователь предоставляет информацию об этом механизме; в самом простом виде это стратификационные веса в табличке, в более сложном — функция меры склонности, зависящая от Y.

Графически этот результат можно проиллюстрировать следующим образом. На рисунке изображён закон условного распределения \(\mathbb{E}(Y \mid X)\) (пунктирная линия) и его МНК-оценка, а также точки наблюдений выборки, по которой получена эта оценка.

Состоятельность оценки при экзогенной и эндогенной стратификации

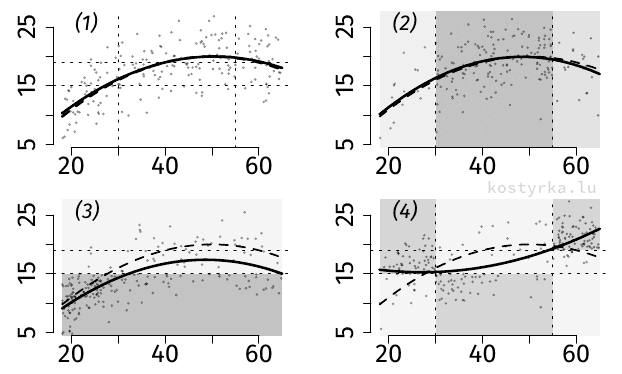
Источник: гнусное самоцитирование.

На рисунке (1) показана оценка на случайной выборке; она состоятельная.
На рисунке (2) показана экзогенная стратификация — по значениям регрессора X: из среднего региона берётся больше наблюдений, чем из крайних; при игнорировании этой стратификации оценка \(\mathbb{E}(Y \mid X)\) остаётся состоятельной, несмотря на то что оценка безусловного математического ожидания \(\mathbb{E}X\) будет смещённой.
На рисунке (3) показана эндогенная стратификация — по значениям зависимой переменной Y: из верхнего региона берётся меньше наблюдений, чем из нижнего. Из-за игнорирования этой стратификации оценка условного математического ожидания \(\mathbb{E}(Y \mid X)\) теряет состоятельность и становится смещённой вниз; это отражается и в оценках параметров линейной регрессии, дающих более низкую линию.
На рисунке (4) показано, что если игнорировать более сложные схемы стратификации и механизмы отбора, то тогда оценки зависимостей могут быть искажены как угодно в любом направлении, а оценки условных математических ожиданий будут по большей части продиктованы соотношениями вероятностей отбора: где больше точек собрали, там и пройдёт линия оценки, чтобы минимизировать меру отклонения модели от реальных наблюдений.

Когорты и исследования «случай — контроль»

Случайные выборки или стратифицированные выборки, которые устраивают исследователя по ключевым характеристикам, для ответа на некоторые вопросы получить невозможно из-за невозможности повернуть время вспять или из-за этических ограничений.

На некоторые вопрос можно с некоторыми оговорками дать ответ, полученный по панельным данным при сравнении когорт. Так, если исследуется уровень счастья и требуется установить наличие или отсутствие каузального эффекта курения, то исследователь может воспользоваться данными панельного обследования и сравнить когорты курящих и некурящих. Самый простой способ — тест на равенство средних, но более правильно использовать структурные модели, где учитывались бы эффекты дополнительных объясняющих переменных и присутствовала бы возможность учесть потенциальную эндогенность («а что если люди курят, потому что они несчастны, а не наоборот?») с помощью инструментов. Если подобная панель получена в рамках крупной кампании по сбору данных, то в ней почти наверняка будут стратификационные веса, содержащие информацию о том, сильно ли отличаются распределения случайных величин в выборке и в генеральной совокупности.

Однако некоторые эффекты нельзя оценить по имеющимся данным, так как нет гипотетической контрольной когорты для сравнения, выборка страдает от смещения отбора, а механизм отбора неизвестен. Такие проблемы часто встречаются в медицине: препарат тестируют не на всех, а только на тех, у кого есть заболевание, и вероятность заболевания может зависеть от факта курения, режима питания, характера работы и прочих потенциально эндогенных переменных. Вероятность заболевания и обращения к врачу также зависит от генов, которые почти невозможно выразить численно в рамках медицинского исследования, но которые могут серьёзно коррелировать почти со всеми наблюдаемыми характеристиками, создавая дополнительный источник эндогенности. Подобные исследования называются «случай — контроль» (ИСК), и основанные на них выводы вида «виагра помогает людям с импотенцией» могут с положительной вероятностью быть истинными, даже если средний возраст испытуемого равен 60, а пол исключительно мужской. Данные выборки не гарантируют несмещённых оценок причинно-следственных связей, однако являются единственной альтернативой тогда, когда для превращения исследования в рандомизированное контролируемое испытание врачу пришлось бы перезаражать половину выборки и не давать ей препаратов.

Итог: «репрезентативная выборка» — источник заблуждений

Заявляю ответственно, что ни один курс или учебник математической статистики не должен в определении выборки содержать слово «репрезентативная». Репрезентативность выборки — тупая, бессмысленная и опасная для студентов-бакалавров концепция, которую на практике в принципе невозможно протестировать, так как ни у кого нет в наличии генеральной совокупности. Можно лишь командным голосом заявить, что выборка по полу и возрасту напоминает генеральную совокупность (так как есть данные переписи населения), а всё остальное — это красивые сновидения исследователя.

Самая-самая честная случайная рандомизированная выборка, являющаяся золотым стандартом в экономических исследованиях и медицинских испытаниях, может отличаться от генеральной совокупности по ряду показателей, и это тем вероятнее, чем больше количество измеряемых показателей.
Если механизм отбора неслучаен, но известен и при этом обратим, то тогда любая выборка, полученная с учётом данного механизма, отлично подходит для исследования, а его выводы можно экстраполировать на генеральную совокупность.
Если механизм отбора наблюдений неслучаен и неизвестен, то выборка может годиться, но с оговоркой, что результаты верны только для тех, кто попал в выборку.

Если кто-то определяет выборку как структуру со свойством репрезентативности, то от него в дальнейшем можно ожидать чего угодно из просроченного арсенала, пылящегося на страницах бесполезных древних учебников, написанных до формализации и критического переосмысления ключевых понятий математической статистики и эконометрики: и предположения фиксированных регрессоров, и совершения колдовских пассов над «матрицами данных» при отсутствии хотя бы первого приближения структурной модели зависимости между случайными переменными, и веры в гомоскедастичность, и требования «нормальности всего», и использования критических значений t-распределения в качестве «точных»...

И я бы не выражался так резко, если бы не пересекался со студентами, которым в 2024 г. в уши вливают всю эту контрпродуктивную лабуду, которая ставит под угрозу валидность любого научного исследования и адекватность результатов. А может, я просто слишком хорошо помню семинары ныне покойного Андрея Александровича Мамонтова, который пресекал на корню наши попытки проблеять какие-то дилетантские версии определений, отправляя нас на пересдачу?..