Сегодня мы оценим часто упоминаемую «логистическую кривую» на данных по выявленным заболевшим коронавирусной инфекцией в разных странах, используя эконометрические и численные методы, и рассчитаем сценарные прогнозы.
В России часто слышится вопрос:
— Когда наша страна пройдёт пик?
Это сложный вопрос, поскольку под «пиком» обычно подразумевается «день с наибольшим количеством новых случаев», и на основе только лишь информации о пике нельзя принять никакие ответственные решения. Более общий вопрос обычно звучит так: «Как будет выглядеть динамика через 2 месяца?» При этом многие статьи — даже вроде бы научные! — говорят о какой-то эфемерной «логистической кривой». Тем не менее, у этой кривой одна проблема: вылезать труднее, чем влезать, поэтому динамика до и после пика может отличаться от зеркальной. Скажите, эти два объекта похожи?
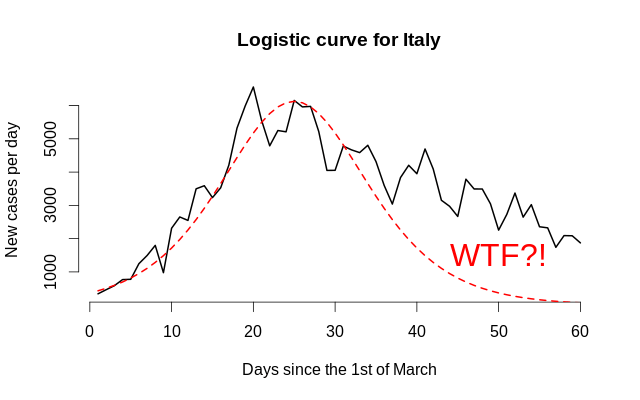
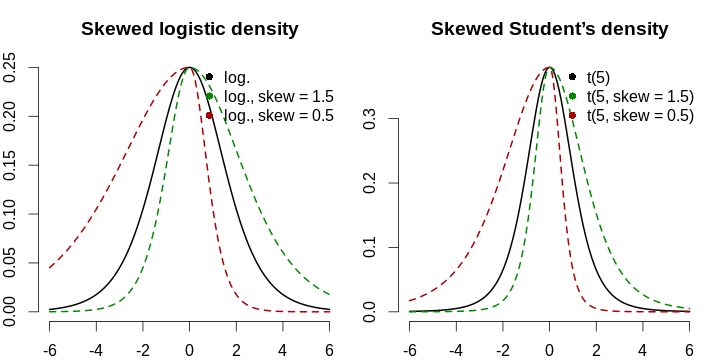
Вот почему асимметрию надо моделировать в явном виде. Мы применим подход, который был использован в работе Fernández & Steel (1998), где авторы обобщают симметричные функции плотности распределения до асимметричных с одним параметром: левая часть растягивается, а правая — сжимается на один и тот же коэффициент, а затем функция нормализуется так, чтобы совпадали первые два момента исходного и нового распределений. Ради лёгкости интерпретации мы ничего не будем нормализовать: мы не моделируем плотность — мы просто берём логистическую кривую и смещаем, масштабируем и скашиваем её, чтобы подогнать под реальные данные. Кроме того, логистическая кривая имеет экспоненциально затухающие хвосты, что не слишком реалистично из-за того, что люди впадают в сладостное забвение, расслабляются, думают, что если в день 10–15 новых случаев, то всё уже закончилось, и начинают слишком близко общаться, и это-то и оборачивается катастрофой. Моделирование тяжести хвоста (скажем, с помощью t-распределения Стьюдента) может быть рассмотрено, однако следует опасаться малого числа наблюдений и вытекающую из этого ненадёжность оценки этого параметра. Формула для обобщённой логистической кривой, описывающей количество новых случаев в день, имеет следующий вид: \[ g(x; \mu, \sigma, s, h) \mathrel{\stackrel{\text{def}}{=}} \begin{cases} h \cdot f \left( \frac{x - \mu}{\sigma \cdot s} \right), & \frac{x - \mu}{\sigma} > 0, \\ h \cdot f \left( \frac{s(x - \mu)}{\sigma} \right), & \frac{x - \mu}{\sigma} \le 0. \end{cases} \] Здесь \(\mu\) — это мода (точка максимума функции, её пик), \(\sigma\) — горизонтальное растяжение, \(s\) — коэффициент скошенности (асимметрии), принимающий значения из диапазона \((0, +\infty)\) и показывающий относительную тяжесть правого хвоста (\(s > 1\) соответствует растяжению правого хвоста ещё правее), а \(h\) отражает вертикальное масштабирование (количество случаев меняется от страны к стране, поэтому абсолютная шкала должна тоже органически проистекать из данных). Помните, что f может быть любой симметричной функцией — мы используем функции, похожие на функции плотности, из соображений теории... и удобства. Нам нужен быстрый и простой ответ!
Для начала скачаем мартовские и апрельские данные с Википедии со страниц вида ‘2020 coronavirus pandemic in X’, где X — название страны. Рассмотрим такие страны, как Испания, Германия, Италия, Люксембург, Швеция, Чехия, Турция и Россия. Собранные данные приводятся в таблице ниже; оговоримся, что это информация на 1 мая 2020 г. и что она может поменяться позже из-за обновления источников или изменения методологии.
| Date | spa | ger | ita | lux | swe | cze | tur | rus |
| 2020-03-01 | 85 | 117 | 1,694 | 0 | 7 | 3 | 0 | 0 |
| 2020-03-02 | 121 | 150 | 2,036 | 0 | 7 | 3 | 0 | 3 |
| 2020-03-03 | 166 | 188 | 2,502 | 0 | 11 | 5 | 0 | 3 |
| 2020-03-04 | 228 | 240 | 3,089 | 0 | 16 | 5 | 0 | 3 |
| 2020-03-05 | 282 | 349 | 3,858 | 2 | 17 | 8 | 0 | 4 |
| 2020-03-06 | 401 | 534 | 4,636 | 3 | 22 | 19 | 0 | 10 |
| 2020-03-07 | 525 | 684 | 5,883 | 4 | 29 | 26 | 0 | 14 |
| 2020-03-08 | 674 | 847 | 7,375 | 5 | 38 | 32 | 0 | 17 |
| 2020-03-09 | 1,231 | 1,112 | 9,172 | 5 | 54 | 38 | 0 | 20 |
| 2020-03-10 | 1,695 | 1,460 | 10,149 | 7 | 108 | 63 | 0 | 20 |
| 2020-03-11 | 2,277 | 1,884 | 12,462 | 7 | 181 | 94 | 1 | 28 |
| 2020-03-12 | 3,146 | 2,369 | 15,113 | 26 | 238 | 116 | 1 | 34 |
| 2020-03-13 | 5,232 | 3,062 | 17,660 | 34 | 266 | 141 | 5 | 45 |
| 2020-03-14 | 6,391 | 3,795 | 21,157 | 51 | 292 | 189 | 6 | 59 |
| 2020-03-15 | 7,988 | 4,838 | 24,747 | 77 | 339 | 298 | 18 | 63 |
| 2020-03-16 | 9,942 | 6,012 | 27,980 | 81 | 384 | 383 | 47 | 93 |
| 2020-03-17 | 11,826 | 7,156 | 31,506 | 140 | 425 | 450 | 98 | 114 |
| 2020-03-18 | 14,769 | 8,198 | 35,713 | 203 | 511 | 560 | 191 | 147 |
| 2020-03-19 | 18,077 | 10,999 | 41,035 | 335 | 603 | 765 | 359 | 199 |
| 2020-03-20 | 21,571 | 13,957 | 47,021 | 484 | 685 | 889 | 670 | 253 |
| 2020-03-21 | 25,496 | 16,662 | 53,578 | 670 | 767 | 1,047 | 947 | 306 |
| 2020-03-22 | 29,909 | 18,610 | 59,138 | 798 | 845 | 1,161 | 1,236 | 367 |
| 2020-03-23 | 35,480 | 22,672 | 63,927 | 875 | 927 | 1,287 | 1,529 | 438 |
| 2020-03-24 | 42,058 | 27,436 | 69,176 | 1,099 | 1,027 | 1,472 | 1,872 | 495 |
| 2020-03-25 | 50,105 | 31,554 | 74,386 | 1,333 | 1,125 | 1,763 | 2,433 | 658 |
| 2020-03-26 | 57,786 | 36,508 | 80,539 | 1,453 | 1,228 | 2,022 | 3,629 | 840 |
| 2020-03-27 | 65,719 | 42,288 | 86,498 | 1,605 | 1,317 | 2,395 | 5,698 | 1,036 |
| 2020-03-28 | 73,232 | 48,582 | 92,472 | 1,831 | 1,392 | 2,657 | 7,402 | 1,264 |
| 2020-03-29 | 80,110 | 52,547 | 97,689 | 1,950 | 1,450 | 2,817 | 9,217 | 1,534 |
| 2020-03-30 | 87,956 | 57,298 | 101,739 | 1,988 | 1,566 | 3,001 | 10,827 | 1,836 |
| 2020-03-31 | 95,923 | 61,913 | 105,792 | 2,178 | 1,683 | 3,308 | 13,531 | 2,337 |
| 2020-04-01 | 104,118 | 67,366 | 110,574 | 2,319 | 1,828 | 3,589 | 15,679 | 2,777 |
| 2020-04-02 | 112,065 | 73,522 | 115,242 | 2,487 | 1,982 | 3,858 | 18,135 | 3,548 |
| 2020-04-03 | 119,199 | 79,696 | 119,827 | 2,612 | 2,179 | 4,190 | 20,921 | 4,149 |
| 2020-04-04 | 126,168 | 85,778 | 124,632 | 2,729 | 2,253 | 4,472 | 23,934 | 4,731 |
| 2020-04-05 | 131,646 | 91,714 | 128,948 | 2,804 | 2,359 | 4,587 | 27,069 | 5,389 |
| 2020-04-06 | 136,675 | 95,391 | 132,547 | 2,843 | 2,566 | 4,822 | 30,217 | 6,343 |
| 2020-04-07 | 141,942 | 99,225 | 135,586 | 2,970 | 2,763 | 5,017 | 34,109 | 7,497 |
| 2020-04-08 | 148,220 | 103,228 | 139,422 | 3,034 | 2,890 | 5,312 | 38,226 | 8,672 |
| 2020-04-09 | 153,222 | 108,202 | 143,626 | 3,115 | 3,036 | 5,569 | 42,282 | 10,131 |
| 2020-04-10 | 158,273 | 113,525 | 147,577 | 3,223 | 3,100 | 5,732 | 47,029 | 11,917 |
| 2020-04-11 | 163,027 | 117,658 | 152,271 | 3,270 | 3,175 | 5,902 | 52,167 | 13,584 |
| 2020-04-12 | 166,831 | 120,479 | 156,363 | 3,281 | 3,254 | 5,991 | 56,956 | 15,770 |
| 2020-04-13 | 170,099 | 123,016 | 159,516 | 3,292 | 3,369 | 6,059 | 61,049 | 18,328 |
| 2020-04-14 | 174,060 | 125,098 | 162,488 | 3,307 | 3,539 | 6,141 | 65,111 | 21,102 |
| 2020-04-15 | 180,659 | 127,584 | 165,155 | 3,373 | 3,665 | 6,301 | 69,392 | 24,490 |
| 2020-04-16 | 184,948 | 130,450 | 168,941 | 3,444 | 3,785 | 6,433 | 74,193 | 27,938 |
| 2020-04-17 | 190,839 | 133,830 | 172,434 | 3,480 | 3,909 | 6,549 | 78,546 | 32,008 |
| 2020-04-18 | 194,416 | 137,439 | 175,925 | 3,537 | 3,964 | 6,654 | 82,329 | 36,793 |
| 2020-04-19 | 198,674 | 139,897 | 178,972 | 3,550 | 4,027 | 6,746 | 86,306 | 42,853 |
| 2020-04-20 | 200,210 | 141,672 | 181,228 | 3,558 | 4,173 | 6,900 | 90,980 | 47,121 |
| 2020-04-21 | 204,178 | 143,457 | 183,957 | 3,618 | 4,284 | 7,033 | 95,591 | 52,763 |
| 2020-04-22 | 208,389 | 145,694 | 187,327 | 3,654 | 4,406 | 7,132 | 98,674 | 57,999 |
| 2020-04-23 | 213,024 | 148,046 | 189,973 | 3,665 | 4,515 | 7,187 | 101,790 | 62,773 |
| 2020-04-24 | 219,764 | 150,383 | 192,994 | 3,695 | 4,610 | 7,273 | 104,912 | 68,622 |
| 2020-04-25 | 223,759 | 152,438 | 195,351 | 3,711 | 4,686 | 7,352 | 107,773 | 74,588 |
| 2020-04-26 | 226,629 | 154,175 | 197,675 | 3,723 | 4,756 | 7,404 | 110,130 | 80,949 |
| 2020-04-27 | 229,422 | 155,193 | 199,414 | 3,729 | 4,884 | 7,445 | 112,261 | 87,147 |
| 2020-04-28 | 232,128 | 156,337 | 201,505 | 3,741 | 4,980 | 7,504 | 114,653 | 93,558 |
| 2020-04-29 | 236,899 | 157,641 | 203,591 | 3,769 | 5,040 | 7,579 | 117,589 | 99,399 |
| 2020-04-30 | 239,369 | 159,119 | 205,463 | 3,784 | 5,051 | 7,682 | 120,204 | 106,498 |
Теперь мы должны выбрать метод оценивания. В принципе, для каждой страны у нас есть пары наблюдений \((1, Y_1), (2, Y_2), \ldots, (61, Y_{61})\), и предполагается, что функциональная форма известна с точностью до 4 (логистическая) или 5 (Стьюдент) параметров. Самым очевидным способом получения оценки является минимизация некоторой штрафной статистики, основанной на функции от расхождений между реальными данными и предсказаниями модели; самый простой случай — это сумма (или среднее) квадратов остатков. Однако на практике часто используются более робастные штрафные функции, а иногда и более робастные статистики, поэтому мы также попробуем для получения оценки параметров проминимизировать по оным сумму модулей (абсолютных отклонений, как в нелинейной квантильной регрессии), а также медиану квадратов ошибок (как в регрессии наименьшей медианы квадратов авторства Rousseeuw). Мы будем минимизировать эти 3 критерия. Обратите внимание, что последний из них не является гладким по параметрам, поэтому может существовать целый континуум значений параметров, дающий одно и то же значение критерия (даже глобальный минимум). \[ C_1 = \frac{1}{n} \sum_{t=1}^T (Y_t - g(t; \theta))^2, \quad C_2 = \frac{1}{n} \sum_{t=1}^T |Y_t - g(t; \theta)|, \quad C_3 = \mathrm{median}[(Y_t - g(t; \theta))^2] \] В-третьих, поскольку мы моделируем параметрические кривые с четырьмя параметрами, нужно прикинуть приблизительные оценки, чтобы близко угадать динамику. Все вышеописанные критерии нелинейны по параметрам, поэтому мы вручную подберём реалистичные значения для каждой из стран, а затем размахнёмся от них вверх-вниз, сделаем просторный гиперкуб и попробуем с помощью стохастического оптимизатора найти в нём точку-кандидата для оптимума. После этого мы доведём его в точный максимум с помощью оптимизатора Нельдера—Мида (с добавлением разумных ограничений).
Запрограммируем общую кривую с помощью нашей собственной функции, которая будет принимать на вход независимую переменную времени (количество дней, прошедших с 1 марта), тип распределения (логистическое или Стьюдента, но при наличии времени и желания можно прописать любые) и параметры этого распределения (вектор длины 4 или 5: пик, горизонтальный масштаб, скошенность, вертикальный масштаб, а для распределения Стьюдента — количество степеней свободы).
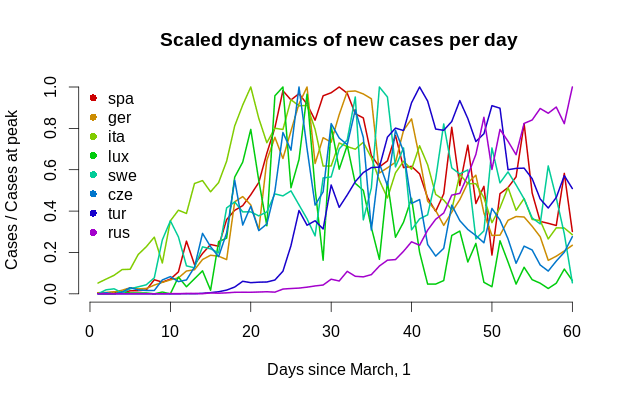
Отметим, что это не функция плотности и что не нужно думать, что для неё будут выполняться свойства логистического или t-распределения, так как она имеет другой масштаб, и вообще, это просто кривая, которая соответствует количеству людей, то есть случаев заболевания. Так выглядит динамика для всех стран на одном графике.
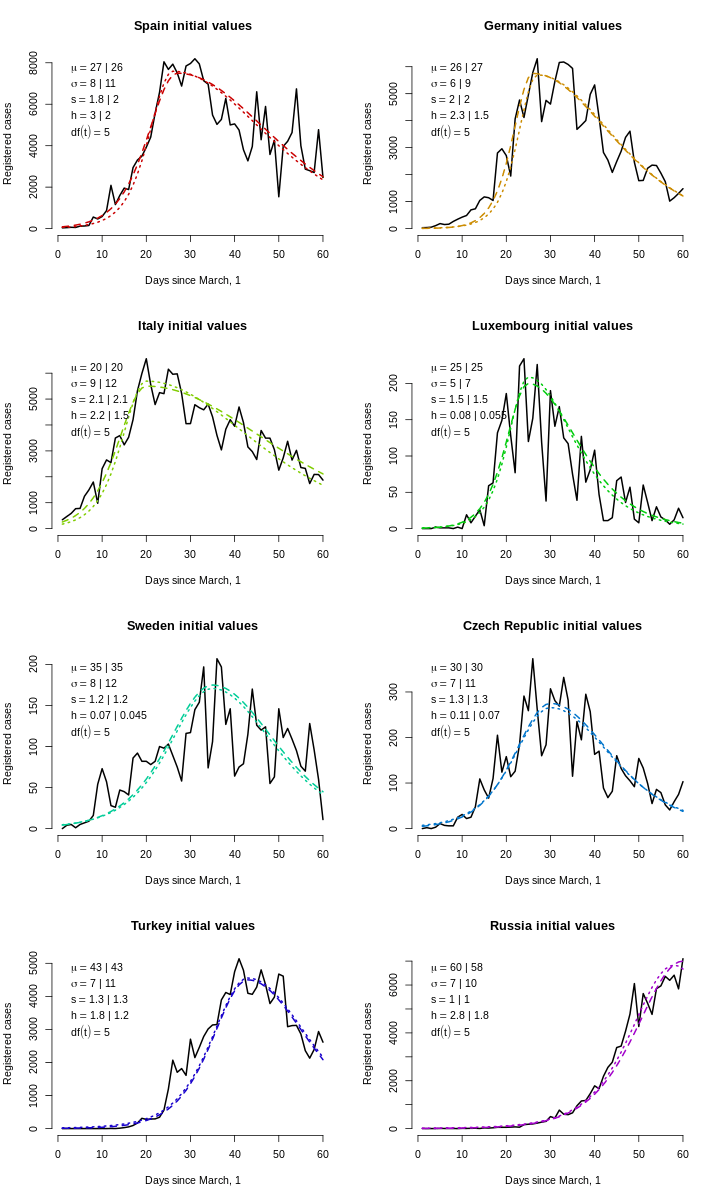
Теперь выберем хорошие стартовые значения для оптимизатора. Для численной стабильности (особенно в градиентных методах) желательно, чтобы у всех параметров был один и тот же порядок величины (можно всё перемасштабировать), и параметр вертикального масштаба, который измеряет людей, гуляет где-то в тысячах или десятках тысяч, поэтому поделим его на 10 000. Для каждой страны мы прикинули на глаз параметры \((\tilde \mu, \tilde\sigma, \tilde s, \tilde h\ [, \widetilde{df}])\), а для стохастического оптимизатора будем использовать гиперкуб, пропорциональный нашим прикидкам: от \((\tilde\mu/2, \tilde\sigma/3, \tilde s/3, \tilde h / 4\ [, 0.1])\) до \((1.5\tilde\mu, 3\tilde\sigma, 3\tilde s, 3\tilde h\ [, 50])\).
Для оптимизации мы используем пакет hydroPSO, так как в нём всё великолепно параллелизуется и гибко настраивается. Пространства высокой размерности становятся более разреженными быстрее, чем кажется, поэтому для плотного из покрытия мы используем начальную популяцию точек размером 400 или 600. Сходимость довольно быстрая для логистической модели и более медленная для модели Стьюдента, поэтому мы используем 50–100 итераций для первой и 75–125 итераций для второй (это всё же грубая предварительная оценка первого шага). Одна итерация занимает 0,25–0,5 секунды, поэтому оценка всех моделей заняла 8 ⋅ (50 + 75 + 100 + 75 + 100 + 125) ⋅ 0,35 ≈ 1500 секунд, или примерно полчаса, — такова цена снижения риска скатывания в локальный оптимум.
Вы думаете, что всё прямо так сразу можно оценить?.. Не тут-то было!
Нам мешает одно яблочко... то есть облачко на горизонте: пока что в России не было пика! Это создаёт ворох проблем: строго говоря, параметр асимметрии и параметр масштаба вместе не идентифицированы, поскольку мы наблюдаем только левую часть распределения: можно умножить параметр асимметрии на 2 и параметр масштабирования на 2 и получить абсолютно такой же левый хвост. В этом случае опасно надеяться, что в самом правом конце данных содержится пик. Известный факт, что оценивание параметров усечённого нормального распределения, когда среднее лежит за пределами диапазона усечения, очень ненадёжно; в нашей ситуации пик также находится за пределами диапазона, что усугубляет положение. Это означает, что получения оценок для России параметр асимметрии должен быть зафиксирован (как параметр других стран), поэтому будет оцениваться только горизонтальный масштаб. Например, если бы у России была динамика затухания, как в Люксембурге, то каким было бы общее число случаев? Иными словами, мы можем делать сценарные прогнозы: турецкий сценарий, итальянский сценарий, среднеевропейский сценарий.
Максимизация второго шага из возможного решения считается за мгновение, и оценки не сильно меняются. Однако результаты оказались более нестабильными для Швеции, одна модель дала странные результаты для Турции, а в случае в Россией вообще всё поехало — потому что мы ещё не применили трюк с фиксированием параметра.
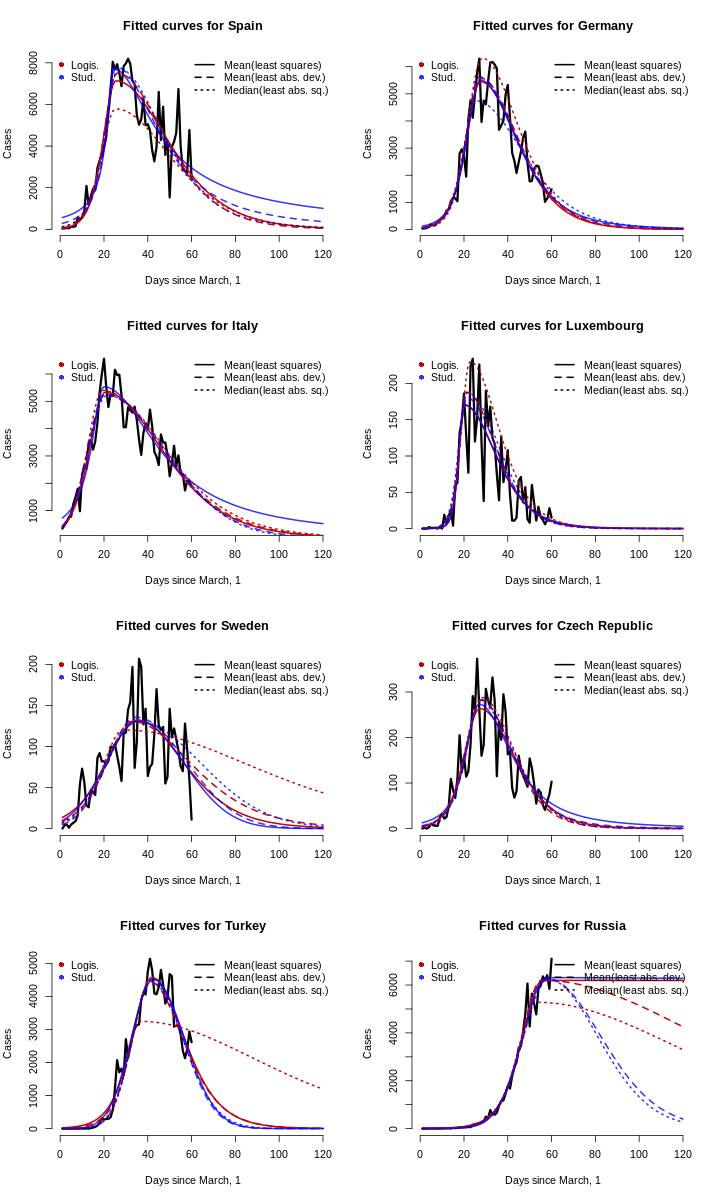
Видим, что среди оценённых моделей нет явного лидера, так как и логистическая, так и стьюдентовская подгонка дают примерно одинаковые результаты. Воспользуемся принципом бритвы Оккама и во избежание перепараметризации ограничим наш анализ только логистическим распределеним и забудем про оценку тяжести хвостов.
Не будем также делать и статистическую инференцию. Конечно, для оценки нелинейного метода наименьших квадратов можно вычислить робастные стандартные ошибки, но для этих данных нетривиально сделать это для двух других оценивателей, данные являются зависимыми во времени, поэтому нет очевидного решения. Наша цель — быть проще.
Вот и настал момент, которого все ждали с нетерпением: сколько же случаев заболевания коронавирусной инфекцией ожидается в России в 2020 году? Когда настанет тот день, когда будет ожидаться менее одного нового заболевшего? Ещё лучше, когда ждать менее чем одного случая в течение двух недель (то есть 1/14 случаев в день), и каково будет количество случаев до этой даты — когда закончится пандемия? Для этого мы можем вызвать вычислить очень простую вещь: идти вправо во времени до тех пор, пока наша функция прироста случаев с оценёнными параметрами не примет значение 1 или 1/14. Общее ожидаемое количество инфицированных будет кумулятивной суммой вплоть до этой даты.
Помните, мы рассматриваем только логистические модели для прогнозирования количества случаев в каждой стране до дня, когда будет менее 1 случая или менее 1/14 случаев в день. Для каждой страны мы выбираем в качестве лучшей модели (из трёх логистических с разными оценивателями) ту, которая точнее всего предсказывает общее количество случаев по состоянию на последнюю дату (то есть на конец выборки, 30 апреля).
| Случаев к 30 апреля | Сред. наименьш. квадр. | Сред. наименьш. модулей | Медиан. наименьш. квадратов | |
| Испания | 239,369 | 237,304 | 242,555 | 203,910 |
| Германия | 159,119 | 158,465 | 164,505 | 183,371 |
| Италия | 205,463 | 203,246 | 204,339 | 212,175 |
| Люксембург | 3,784 | 3,749 | 4,108 | 5,147 |
| Швеция | 5,051 | 5,076 | 5,046 | 5,160 |
| Чехия | 7,682 | 7,646 | 7,710 | 8,033 |
| Турция | 120,204 | 121,944 | 116,104 | 102,600 |
| Итого к 30 апреля | Дней с 1 марта до 1 чел./д. | Дней с 1 марта до 1 чел./14 д. | Случаев до 1 чел./д. | Случаев до 1 чел./14 д. | |
| Испания | 239,369 | 189 | 231 | 282,401 | 282,415 |
| Германия | 159,119 | 142 | 172 | 171,369 | 171,379 |
| Италия | 205,463 | 201 | 249 | 241,977 | 241,993 |
| Люксембург | 3,784 | 83 | 109 | 3,838 | 3,847 |
| Швеция | 5,051 | 148 | 196 | 6,752 | 6,768 |
| Чехия | 7,682 | 95 | 120 | 8,029 | 8,037 |
| Турция | 120,204 | 140 | 166 | 145,922 | 145,930 |
| Пик (μ) | Гориз. масшт. (σ) | Скошенность (s) | Верт. масшт. (h) | |
| Испания | 25.383 | 7.859 | 2.026 | 2.854 |
| Германия | 27.533 | 7.050 | 1.612 | 2.180 |
| Италия | 20.519 | 9.619 | 1.881 | 2.103 |
| Люксембург | 20.131 | 3.999 | 2.410 | 0.068 |
| Швеция | 32.858 | 12.033 | 1.519 | 0.052 |
| Чехия | 27.818 | 6.764 | 1.400 | 0.113 |
| Турция | 41.888 | 7.754 | 1.277 | 1.829 |
Но постойте! Забыли про Россию!
У нас 7 стран, значит, 7 разных сценариев. Эти сценарии в терминах параметров описываются днём пика (\(\mu\)), горизонтальным размахом (\(\sigma\)), асимметрией (\(s\)), вертикальным масштабом (\(h\)), а для России мы не можем знать степень асимметрии. Сравните эти два графика.
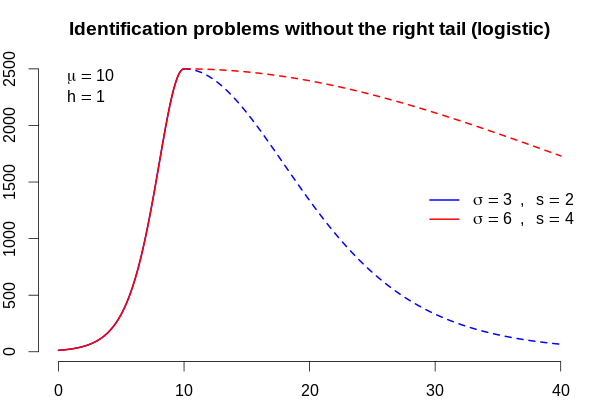
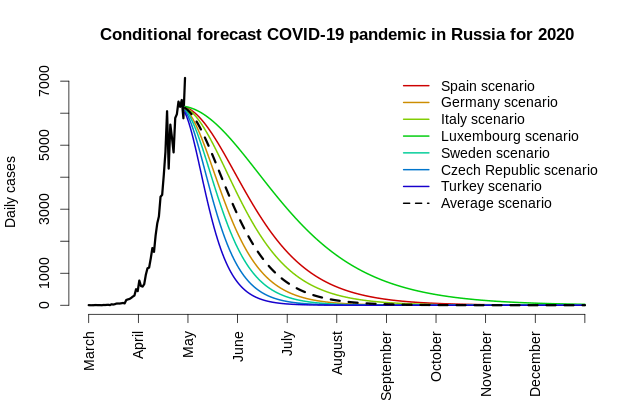
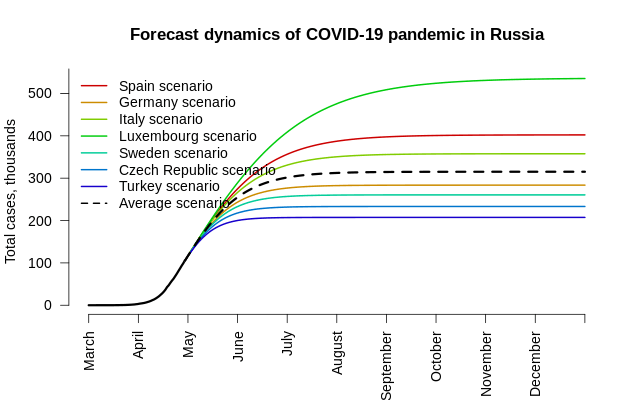
Для одного и того же левого хвоста мы получаем разные правые хвосты: в примере выше красный в 4 раза тяжелее синего. Это очень сильно сказывается на прогнозах: синяя кривая соответствует пандемии, которая затухает до 1 нового случая в день за 66 дней и подкашивает за всё время 37 469 человек, а красная кривая — пандемии, которая тянется 232 дня и охватывает 127 451 случай! Это означает, что начальные значения для России должны быть изменены в соответствии со всеми семью сценариями для других стран.
После переоценки логистической модели для России с асимметрией, зафиксированной на значении 1 (минимизация среднего модуля отклонений дала немного более точное общее число случаев с относительной погрешностью чуть менее 1%), мы можем умножить и \(\sigma\), и \(s\) на оценку параметра \(s\) для других стран, рассчитать два красных дня календаря (менее 1 случая за 1 день или за 14 дней) и получить общее количество случаев.
Оценки для России: \(\hat\mu = 56.1\), \(\hat \sigma / s = 6.33\), \(\hat h = 2.49\). Это означает, что, несмотря на отсутствие чёткого пика на 61-й день, он таки имел быть на 56-й день, непосредственно перед окончанием сбора данных.
| Дней до 1 чел./д. | Дней до 1 чел./14 д. | Случаев до 1 чел./д. | Случаев до 1 чел./14 д. | |
| Сценарий Испании | 320 | 388 | 402,422 | 402,445 |
| Сценарий Германии | 223 | 267 | 283,730 | 283,745 |
| Сценарий Италии | 284 | 343 | 357,887 | 357,907 |
| Сценарий Люксембурга | 429 | 526 | 536,540 | 536,573 |
| Сценарий Швеции | 205 | 243 | 260,712 | 260,724 |
| Сценарий Чехии | 182 | 215 | 233,328 | 233,339 |
| Сценарий Турции | 161 | 188 | 207,443 | 207,452 |
| Средний сценарий (s = 1.73) | 249 | 299 | 315,371 | 315,387 |
Прежде чем перейти к заключению, обязательно оговорим несколько «но»:
- Оценка смещения кривой (\(\hat\mu\)) по левой ея части очень ненадёжна, поэтому вокруг этой оценки существует огромный доверительный интервал. Насколько огромный? Любопытствующий читатель может даже рассчитать стандартные ошибки, но о нормальности оценки не может быть и речи, поскольку хорошо известно, что поведение оценок на границе области допустимых параметров далеко от асимптотически нормального (как, например, метод максимального правдоподобия не работает для оценки экстремальных порядковых статистик).
- Сам пик, который мы определили как максимальное число случаев, соответствует пику сглаженной кривой, даже если отдельные дневные наблюдения могут скакать выше или ниже — предполагается, помимо всего прочего, что в среднем ошибка ноль. Если существует систематическое занижение отчётности из-за недостаточного количества доступных тестов, а реальные цифры выше, то эта упрощённая модель не может дать ничего полезного исходя из имеющихся данных, и требуется использовать другие, более сложные методы.
- Множество бессимптомных случаев, которые мало где регистрируются, составляет подводную часть айсберга, поэтому, если этот невидимый статистике айсберг полностью поднять над уровнем моря, то вершина сместится вправо.
- Дневные цифры сильно зависят от тактики тестирования, хорошей погоды (это не «экономика солнечных пятен» Джевонса, а корреляция с количеством людей, собирающихся на улице), выступлений президента и иных неучтённых переменных.
Все эти оговорки свидетельствуют о том, что полученная нами оценка, скорее всего, недооценивает положение реального пика, но для решения проблем, изложенных выше, нужно обзавестись более качественными пространственными данными, собрать больше информации о плотности населения, географическом распределении — настоящая работа для настоящих эпидемиологов. Выводы — если Россия будет повторять динамику некоторых европейских стран и если забыть вышеизложенные оговорки — таковы:
- Пик, скорее всего, уже наступил — он пришёлся на самый конец апреля 2020 года;
- Общее количество заражённых COVID-19 россиян составит от 200 до 500 тысяч;
- При среднем европейском сценарии и средней асимметрии динамики (при которой уменьшение количества случаев в день после пика примерно в 3 раза медленнее, чем нарастание до пика) общее число случаев в России за всё время составит примерно 315 тысяч;
- Ожидается, что в начале ноября 2020 г. число новых случаев в день станет меньше 1, а к концу декабря будет меньше 1 случая в течение 2 недель.
Только время покажет, насколько точны эти примитивные оценки, поэтому рекомендуется повторить оценивание на новых данных (возможно, на большем количестве стран) и перестроить прогнозы.
Скопируйте приведённую выше таблицу в R в объект ds и используйте приведённый ниже код для репликации результатов из данной статьи.
library(hydroPSO)
library(stargazer)
cs <- c("spa", "ger", "ita", "lux", "swe", "cze", "tur", "rus")
csn <- c("Spain", "Germany", "Italy", "Luxembourg", "Sweden", "Czech Republic", "Turkey", "Russia")
# Uncomment this for Cyrillic names
# csn <- c("Испания", "Германия", "Италия", "Люксембург", "Швеция", "Чехия", "Турция", "Россия")
d <- lapply(cs, function(x) readLines(paste0(x, ".fsf")))
clean <- function(x) {
x <- gsub("\\s+", " ", x)
x <- gsub(" $", "", x)
x <- gsub(",", "", x)
x <- gsub("\\([^)]+\\)", "", x)
x
}
d <- lapply(d, function(x) strsplit(clean(x), " "))
d <- lapply(d, function(y) lapply(y, function(x) if (length(x) == 2) x else x[1:2]) )
d <- lapply(d, function(x) as.data.frame(do.call(rbind, x), stringsAsFactors = FALSE))
d <- lapply(d, function(x) {colnames(x) <- c("Date", "Cases"); x})
ds <- Reduce(
function(x, y) merge(x, y, all = TRUE, by = "Date"),
d
)
colnames(ds) <- c("Date", cs)
for (i in 2:ncol(ds)) {
ds[, i] <- as.numeric(ds[, i])
if (is.na(ds[1, i])) {
nm <- which(is.finite(ds[, i]))[1]
ds[1:(nm-1), i] <- 0
}
}
ds <- ds[1:61, ]
stargazer(ds, type = "html", summary = FALSE, out = "blog.html", rownames = FALSE)
mycurve <- function(x, distrib, pars) {
pars[4] <- pars[4] * 1e4
xstd <- (x - pars[1]) / pars[2]
f <- switch(distrib,
logistic = ifelse(xstd > 0, dlogis(xstd/pars[3]), dlogis(xstd*pars[3])) * pars[4],
student = ifelse(xstd > 0, dt(xstd/pars[3], df = pars[5]), dt(xstd*pars[3], df = pars[5])) * pars[4]
)
return(f)
}
png("plot1-logistic-curve-coronavirus-italy.png", 640, 400, type = "cairo", pointsize = 16)
plot(diff(ds$ita), type = "l", xlab = "Days since the 1st of March", ylab = "New cases per day",
bty = "n", lwd = 2, main = "Logistic curve for Italy")
lines(1:60, mycurve(1:60, "logistic", c(25, 6, 1, 2.45)), col = "red", lty = 2, lwd = 2)
text(50, 1500, "WTF?!", col = "red", cex = 2)
dev.off()
mycols <- c("#000000", "#008800", "#AA0000")
png("plot2-density-logistic-curve-for-corona-virus-flattening.png", 720, 360, pointsize = 16)
par(mar = c(2, 2, 3, 1), mfrow = c(1, 2))
curve(dlogis(x), -6, 6, n = 1001, main = "Skewed logistic density", bty = "n",
lwd = 2, ylim = c(0, dlogis(0)), ylab = "", xlab = "")
curve(mycurve(x, "logistic", c(0, 1, 1.5, 1e-4)), -6, 6, n = 1001, add = TRUE,
col = mycols[2], lwd = 2, lty = 2)
curve(mycurve(x, "logistic", c(0, 1, 0.5, 1e-4)), -6, 6, n = 1001, add = TRUE,
col = mycols[3], lwd = 2, lty = 2)
legend("topright", c("log.", "log., skew = 1.5", "log., skew = 0.5"), col = mycols, pch = 16, bty = "n")
curve(dt(x, 5), -6, 6, n = 1001, main = "Skewed Student’s density", bty = "n",
lwd = 2, ylim = c(0, dt(0, 5)))
curve(mycurve(x, "student", c(0, 1, 1.5, 1e-4, 5)), -6, 6, n = 1001, add = TRUE,
col = mycols[2], lwd = 2, lty = 2)
curve(mycurve(x, "student", c(0, 1, 0.5, 1e-4, 5)), -6, 6, n = 1001, add = TRUE,
col = mycols[3], lwd = 2, lty = 2)
legend("topright", c("t(5)", "t(5, skew = 1.5)", "t(5, skew = 0.5)"), col = mycols, pch = 16, bty = "n")
dev.off()
ds[, (length(cs)+2):(length(cs)*2+1)] <- sapply(ds[, 2:(length(cs)+1)], function(x) diff(c(NA, x)))
colnames(ds)[(length(cs)+2):(length(cs)*2+1)] <- paste0("d", cs)
ds <- ds[2:nrow(ds), ]
mycols <- rainbow(length(cs), end = 0.8, v = 0.8)
png("plot3-new-covid-19-cases-as-a-fraction-of-maximum.png", 640, 400, pointsize = 16)
plot(NULL, NULL, xlim = c(1, nrow(ds)), ylim = c(0, 1), xlab = "Days since March, 1",
ylab = "Cases / Cases at peak", bty = "n", main = "Scaled dynamics of new cases per day")
for (i in (length(cs)+2):(length(cs)*2+1)) lines(ds[, i] / max(ds[, i]),
type = "l", lwd = 2, col = mycols[i - length(cs) - 1])
legend("topleft", cs, pch = 16, col = mycols, bty = "n")
dev.off()
start.pars <- list(list(c(27, 8, 1.8, 3), c(26, 11, 2, 2, 5)), # Spain
list(c(26, 6, 2, 2.3), c(27, 9, 2, 1.5, 5)), # Germany
list(c(20, 9, 2.1, 2.2), c(20, 12, 2.1, 1.5, 5)), # Italy
list(c(25, 5, 1.5, 0.08), c(25, 7, 1.5, 0.055, 5)), # Luxembourg
list(c(35, 8, 1.2, 0.07), c(35, 12, 1.2, 0.045, 5)), # Sweden
list(c(30, 7, 1.3, 0.11), c(30, 11, 1.3, 0.07, 5)), # Czech,
list(c(43, 7, 1.3, 1.8), c(43, 11, 1.3, 1.2, 5)), # Turkey
list(c(60, 7, 1, 2.8), c(58, 10, 1, 1.8, 5)) # Russia
)
start.pars <- lapply(start.pars, function(x) {names(x) <- c("logistic", "student"); x})
leg <- function(i) {
c(parse(text = paste0('mu == ', start.pars[[i]][[1]][1], '*" | "*', start.pars[[i]][[2]][1])),
parse(text = paste0('sigma == ', start.pars[[i]][[1]][2], '*" | "*', start.pars[[i]][[2]][2])),
parse(text = paste0('s == ', start.pars[[i]][[1]][3], '*" | "*', start.pars[[i]][[2]][3])),
parse(text = paste0('h == ', start.pars[[i]][[1]][4], '*" | "*', start.pars[[i]][[2]][4])),
parse(text = paste0('df(t) == ', start.pars[[i]][[2]][5])))
}
png("plot4-initial-values-for-search.png", 720, 1200, pointsize = 16)
par(mfrow = c(4, 2))
for (i in 1:length(cs)) {
plot(ds[, paste0("d", cs[i])], type = "l", lwd = 2,
xlab = "Days since March, 1", ylab = "Registered cases", bty = "n",
main = paste0(csn[i], " initial values"), ylim = c(0, max(ds[, paste0("d", cs[i])])))
lines(mycurve(1:nrow(ds), "logistic", start.pars[[i]][[1]]), col = mycols[i], lwd = 2, lty = 2)
lines(mycurve(1:nrow(ds), "student", start.pars[[i]][[2]]), col = mycols[i], lwd = 2, lty = 3)
legend("topleft", legend = leg(i), bty = "n")
}
dev.off()
criterion <- function(pars, observed, distrib, fun = function(x) mean(x^2)) {
theor <- mycurve(x = 1:length(observed), distrib = distrib, pars = pars)
return(fun(theor - observed))
}
rls <- function(x) sqrt(mean(x^2)) # Root mean least square; root is here for the purposes of comparison
nla <- function(x) mean(abs(x))
nms <- function(x) sqrt(median(x^2)) # Root median of squares
opt.res <- vector("list", length(cs))
for (i in 1:length(cs)) {
sl <- start.pars[[i]][[1]]
st <- start.pars[[i]][[2]]
ll <- start.pars[[i]][[1]] / c(2, 3, 3, 4) # Lower bound for logistic
ul <- start.pars[[i]][[1]] * c(1.5, 3, 3, 3) # Upper bound for logistic
lt <- c(start.pars[[i]][[2]][1:4] / c(2, 3, 3, 4), 0.1) # Lower bound for Student
ut <- c(start.pars[[i]][[2]][1:4] * c(1.5, 3, 3, 3), 50) # Upper bound for Student
contl1 <- list(npart = 400, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 50, plot = TRUE)
contl2 <- list(npart = 400, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 75, plot = TRUE)
contl3 <- list(npart = 400, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 100, plot = TRUE)
contt1 <- list(npart = 600, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 75, plot = TRUE)
contt2 <- list(npart = 600, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 100, plot = TRUE)
contt3 <- list(npart = 600, REPORT = 1, parallel = "parallel", par.nnodes = 6, maxit = 125, plot = TRUE)
set.seed(1); cat(csn[i], "logistic: least squares\n")
opt.log.nls <- hydroPSO(par = sl, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", rls),
lower = ll, upper = ul, control = contl1)
set.seed(1); cat(csn[i], "logistic: least absolute deviations\n")
opt.log.nla <- hydroPSO(par = sl, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", nla),
lower = ll, upper = ul, control = contl2)
set.seed(1); cat(csn[i], "logistic: median of least squares\n")
opt.log.nms <- hydroPSO(par = sl, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", nms),
lower = ll, upper = ul, control = contl3)
set.seed(1); cat(csn[i], "student: least squares\n")
opt.t.nls <- hydroPSO(par = st, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "student", rls),
lower = lt, upper = ut, control = contt1)
set.seed(1); cat(csn[i], "student: least absolute deviations\n")
opt.t.nla <- hydroPSO(par = st, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "student", nla),
lower = lt, upper = ut, control = contt2)
set.seed(1); cat(csn[i], "student: median of least squares\n")
opt.t.nms <- hydroPSO(par = st, fn = function(x) criterion(x, ds[, paste0("d", cs[i])], "student", nms),
lower = lt, upper = ut, control = contt3)
opt.res[[i]] <- list(opt.log.nls, opt.log.nla, opt.log.nms, opt.t.nls, opt.t.nla, opt.t.nms)
save(opt.res, file = "opt.RData", compress = "xz")
}
ui4 <- diag(4)
ci4 <- c(10, 1, 0.01, 1e-5)
ui5 <- diag(5)
ci5 <- c(10, 1, 0.01, 1e-5, 0.1)
opt.refined <- vector("list", length(cs))
for (i in 1:length(cs)) {
cat(csn[i], "\n")
sl1 <- opt.res[[i]][[1]]$par # Replace with start.pars[[i]]$logistic if you did not do the stochastic optimisation
sl2 <- opt.res[[i]][[2]]$par # Replace with start.pars[[i]]$logistic if you did not do the stochastic optimisation
sl3 <- opt.res[[i]][[3]]$par # Replace with start.pars[[i]]$logistic if you did not do the stochastic optimisation
st1 <- opt.res[[i]][[4]]$par # Replace with start.pars[[i]]$student if you did not do the stochastic optimisation
st2 <- opt.res[[i]][[5]]$par # Replace with start.pars[[i]]$student if you did not do the stochastic optimisation
st3 <- opt.res[[i]][[6]]$par # Replace with start.pars[[i]]$student if you did not do the stochastic optimisation
opt.log.nls <- constrOptim(sl1, function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", rls),
grad = NULL, ui = ui4, ci = ci4, outer.iterations = 300)
opt.log.nla <- constrOptim(sl2, function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", nla),
grad = NULL, ui = ui4, ci = ci4, outer.iterations = 300)
opt.log.nms <- constrOptim(sl3, function(x) criterion(x, ds[, paste0("d", cs[i])], "logistic", nms),
grad = NULL, ui = ui4, ci = ci4, outer.iterations = 300)
opt.t.nls <- constrOptim(st1, function(x) criterion(x, ds[, paste0("d", cs[i])], "student", rls),
grad = NULL, ui = ui5, ci = ci5, outer.iterations = 300)
opt.t.nla <- constrOptim(st2, function(x) criterion(x, ds[, paste0("d", cs[i])], "student", nla),
grad = NULL, ui = ui5, ci = ci5, outer.iterations = 300)
opt.t.nms <- constrOptim(st2, function(x) criterion(x, ds[, paste0("d", cs[i])], "student", nms),
grad = NULL, ui = ui5, ci = ci5, outer.iterations = 300)
opt.refined[[i]] <- list(opt.log.nls, opt.log.nla, opt.log.nms, opt.t.nls, opt.t.nla, opt.t.nms)
}
save(opt.res, opt.refined, file = "opt.RData", compress = "xz")
xmax <- 120
xinf <- 1000
mycols <- c("#CC0000", "#0000FFCC")
png("plot5-fitted-logistic-curve-total-infected-coronavirus-cases.png", 720, 1200, type = "cairo", pointsize = 16)
par(mfrow = c(4, 2))
for (i in 1:length(cs)) {
plot(ds[, paste0("d", cs[i])], xlim = c(1, xmax), type = "l", lwd = 3,
xlab = "Days since March, 1", ylab = "Cases", bty = "n", main = paste0("Fitted curves for ", csn[i]))
for (j in 1:3) {
lines(mycurve(1:xmax, distrib = "logistic", pars = opt.refined[[i]][[j]]$par), lwd = 2, lty = j, col = mycols[1])
lines(mycurve(1:xmax, distrib = "student", pars = opt.refined[[i]][[j + 3]]$par), lwd = 2, lty = j, col = mycols[2])
}
legend("topleft", c("Logis.", "Stud."), pch = 16, col = mycols, bty = "n")
legend("topright", c("Mean(least squares)", "Mean(least abs. dev.)", "Median(least abs. sq.)"),
lty = 1:3, lwd = 2, bty = "n")
}
dev.off()
res.tab <- vector("list", length(cs))
for (i in 1:length(cs)) {
cat(csn[i])
a <- cbind(c(start.pars[[i]]$logistic, NA), c(opt.refined[[i]][[1]]$par, NA),
c(opt.refined[[i]][[2]]$par, NA), c(opt.refined[[i]][[3]]$par, NA),
start.pars[[i]]$student, opt.refined[[i]][[4]]$par,
opt.refined[[i]][[5]]$par, opt.refined[[i]][[6]]$par)
colnames(a) <- c("Log. init. val.", "Log. LS", "Log. LAD", "Log. LMS",
"Stud. init. val.", "Stud. LS", "Stud. LAD", "Stud. LMS")
row.names(a) <- c("Peak", "Horiz. scale", "Skew", "Vert. scale", "Stud. DoF")
res.tab[[i]] <- a
# stargazer(a, out = paste0(csn[i], ".html"), type = "html", summary = FALSE, digits = 2)
}
find.day <- function(cases, distrib, pars) {
uniroot(function(x) mycurve(x, distrib, pars) - cases,
lower = pars[1], upper = pars[1] + 180, extendInt = "downX", maxiter = 200, tol = 1e-8)$root
}
get.cases <- function(xmax, distrib, pars) {
round(sum(mycurve(1:xmax, distrib, pars)))
}
days.to.one <- days.to.tw <- cases.one <- cases.tw <- cases.insample <- matrix(NA, nrow = length(cs), ncol = 6)
best.mod <- best.log <- numeric(length(cs))
for (i in 1:length(cs)) {
days.to.one[i, ] <- c(sapply(1:3, function(j) find.day(1, "logistic", opt.refined[[i]][[j]]$par)),
sapply(4:6, function(j) find.day(1, "student", opt.refined[[i]][[j]]$par)))
days.to.tw[i, ] <- c(sapply(1:3, function(j) find.day(1/14, "logistic", opt.refined[[i]][[j]]$par)),
sapply(4:6, function(j) find.day(1/14, "student", opt.refined[[i]][[j]]$par)))
cases.one[i, ] <- c(sapply(1:3, function(j) get.cases(ceiling(days.to.one[i, j]), "logistic", opt.refined[[i]][[j]]$par)),
sapply(4:6, function(j) get.cases(ceiling(days.to.one[i, j]), "student", opt.refined[[i]][[j]]$par)))
cases.tw[i, ] <- c(sapply(1:3, function(j) get.cases(ceiling(days.to.tw[i, j]), "logistic", opt.refined[[i]][[j]]$par)),
sapply(4:6, function(j) get.cases(ceiling(days.to.tw[i, j]), "student", opt.refined[[i]][[j]]$par)))
cases.insample[i, ] <- c(sapply(1:3, function(j) get.cases(nrow(ds), "logistic", opt.refined[[i]][[j]]$par)),
sapply(4:6, function(j) get.cases(nrow(ds), "student", opt.refined[[i]][[j]]$par)))
best.mod[i] <- which.min(abs(ds[nrow(ds), cs[i]] - cases.insample[i, ]))
best.log[i] <- which.min(abs(ds[nrow(ds), cs[i]] - cases.insample[i, 1:3]))
cat(csn[i], "has the best in-sample fit from model", best.mod[i], "and among logistic models,", best.log[i], "\n")
}
colnames(days.to.one) <- colnames(days.to.tw) <- c("Log. LS", "Log. LAD", "Log. LMS", "Stud. LS", "Stud. LAD", "Stud. LMS")
row.names(days.to.one) <- row.names(days.to.tw) <- csn
mod.inds <- c("Mean least squares", "Mean abs. dev.", "Median least sq.")
cases.ins <- cbind(as.numeric(ds[nrow(ds), 2:(length(cs))]), cases.insample[1:7, 1:3])
colnames(cases.ins) <- c("Real cases by April, 30", paste0(mod.inds, " forecast"))
row.names(cases.ins) <- csn[1:7]
stargazer(cases.ins, type = "html", out = "insample.html", summary = FALSE)
best.log
best.pars <- lapply(1:7, function(i) opt.refined[[i]][[best.log[i]]]$par)
best.pars <- do.call(rbind, best.pars)
row.names(best.pars) <- csn[1:7]
colnames(best.pars) <- c("Peak (mu)", "Horiz. scale (sigma)", "Skewness (s)", "Vert. scale (h)")
stargazer(best.pars, type = "html", out = "bestpars.html", summary = FALSE)
days.to <- ceiling(cbind(sapply(1:7, function(i) days.to.one[i, best.log[i]]),
sapply(1:7, function(i) days.to.tw[i, best.log[i]])))
cases <- ceiling(cbind(sapply(1:7, function(i) cases.one[i, best.log[i]]),
sapply(1:7, function(i) cases.tw[i, best.log[i]])))
dcases <- cbind(as.numeric(ds[nrow(ds), 2:length(cs)]), days.to, cases)
colnames(dcases) <- c("Cases by April, 30", "Days from March, 1 till 1 new case/day",
"Days from March, 1 till 1 new case/14 days",
"Cases till 1 new case/day", "Cases till 1 new case/14 days")
row.names(dcases) <- csn[1:7]
stargazer(dcases, type = "html", out = "days-to-one.html", summary = FALSE)
png("plot6-density-logistic-curve-yielding-different-tails.png", 600, 400, pointsize = 16)
par(mar = c(2, 2, 3, 1))
curve(mycurve(x, "logistic", c(10, 3, 2, 1)), 0, 10, n = 1001, col = "blue",
lwd = 2, bty = "n", xlab = "n", ylab = "n",
main = "Identification problems without the right tail (logistic)", xlim = c(0, 40))
curve(mycurve(x, "logistic", c(10, 6, 4, 1)), 0, 10, n = 1001, add = TRUE, col = "red", lwd = 2)
curve(mycurve(x, "logistic", c(10, 3, 2, 1)), 10, 40, n = 1001, add = TRUE, col = "blue", lwd = 2, lty = 2)
curve(mycurve(x, "logistic", c(10, 6, 4, 1)), 10, 40, n = 1001, add = TRUE, col = "red", lwd = 2, lty = 2)
legend("right", c(expression(sigma == 3 ~ ", " ~ s == 2), expression(sigma == 6 ~ ", " ~ s == 4)),
bty = "n", col = c("blue", "red"), lwd = 2)
legend("topleft", c(expression(mu == 10), expression(h == 1)), bty = "n")
dev.off()
d.good <- find.day(1, "logistic", c(10, 3, 2, 1))
d.bad <- find.day(1, "logistic", c(10, 6, 4, 1))
get.cases(ceiling(d.good), "logistic", c(10, 3, 2, 1))
get.cases(ceiling(d.bad), "logistic", c(10, 6, 4, 1))
criterion.log.rest <- function(pars, skew, observed, fun = function(x) mean(x^2)) {
theor <- mycurve(x = 1:length(observed), distrib = "logistic", pars = c(pars[1:2], skew, pars[3]))
return(fun(theor - observed))
}
set.seed(1); cat("Russia logistic: least squares\n")
opt.log.nls <- hydroPSO(par = start.pars[[8]]$logistic,
fn = function(x) criterion.log.rest(x, 1, ds[, "drus"], rls),
lower = start.pars[[8]]$logistic[c(1, 2, 4)] / 4,
upper = start.pars[[8]]$logistic[c(1, 2, 4)] * 4, control = contt3)
set.seed(1); cat("Russia logistic: least absolute deviations\n")
opt.log.nla <- hydroPSO(par = start.pars[[8]]$logistic[c(1, 2, 4)],
fn = function(x) criterion.log.rest(x, 1, ds[, "drus"], nla),
lower = start.pars[[8]]$logistic[c(1, 2, 4)] / 4,
upper = start.pars[[8]]$logistic[c(1, 2, 4)] * 4, control = contt3)
rus.nls <- c(opt.log.nls$par[1:2], 1, opt.log.nls$par[3])
rus.nla <- c(opt.log.nla$par[1:2], 1, opt.log.nla$par[3])
rus.nls.cases <- get.cases(nrow(ds), "logistic", rus.nls)
rus.nla.cases <- get.cases(nrow(ds), "logistic", rus.nla)
c(ds[nrow(ds), "rus"], ds[nrow(ds), "rus"] - rus.nls.cases, ds[nrow(ds), "rus"] - rus.nla.cases)
# Least absolute deviations is better
russia <- matrix(NA, nrow = 8, ncol = 4)
mycols <- rainbow(length(cs), end = 0.8, v = 0.8)
for (i in 1:7) {
these.pars <- c(rus.nla[1], rus.nla[2] * best.pars[i, 3], best.pars[i, 3], rus.nla[4])
to1 <- ceiling(find.day(1, "logistic", these.pars))
to14 <- ceiling(find.day(1/14, "logistic", these.pars))
c1 <- get.cases(to1, "logistic", these.pars)
c14 <- get.cases(to14, "logistic", these.pars)
russia[i, ] <- c(to1, to14, c1, c14)
}
these.pars <- c(rus.nla[1], rus.nla[2] * mean(best.pars[, 3]), mean(best.pars[, 3]), rus.nla[4])
to1 <- ceiling(find.day(1, "logistic", these.pars))
to14 <- ceiling(find.day(1/14, "logistic", these.pars))
c1 <- get.cases(to1, "logistic", these.pars)
c14 <- get.cases(to14, "logistic", these.pars)
russia[8, ] <- c(to1, to14, c1, c14)
png("plot7-russia-coronavirus-covid-19-cases-forecast-daily.png", 640, 400, pointsize = 14)
plot(ds[, "drus"], xlim = c(1, 305), ylim = c(0, max(ds[, "drus"])), type = "l",
lwd = 3, bty = "n", main = "Conditional forecast COVID-19 pandemic in Russia for 2020",
xlab = "", ylab = "Daily cases", xaxt = "n")
axis(1, seq(1, 305, length.out = 11), c(month.name[3:12], ""), las = 2)
for (i in 1:7) {
these.pars <- c(rus.nla[1], rus.nla[2] * best.pars[i, 3], best.pars[i, 3], rus.nla[4])
lines(nrow(ds):305, mycurve(nrow(ds):305, "logistic", these.pars), lwd = 2, col = mycols[i])
}
these.pars <- c(rus.nla[1], rus.nla[2] * mean(best.pars[, 3]), mean(best.pars[, 3]), rus.nla[4])
lines(nrow(ds):305, mycurve(nrow(ds):305, "logistic", these.pars), lwd = 3, lty = 2, col = "black")
legend("topright", paste0(c(csn[1:7], "Average"), " scenario"),
col = c(mycols[1:7], "black"), lwd = 2, lty = c(rep(1, 7), 2), bty = "n")
dev.off()
png("plot8-russia-coronavirus-covid-19-cases-forecast-cumulative.png", 640, 400, pointsize = 14)
plot(cumsum(ds[, "drus"]), xlim = c(1, 305), ylim = c(0, max(russia)),
type = "l", lwd = 3, bty = "n", main = "Forecast dynamics of COVID-19 pandemic in Russia",
xlab = "", ylab = "Total cases, thousands", xaxt = "n", yaxt = "n")
axis(1, seq(1, 305, length.out = 11), c(month.name[3:12], ""), las = 2)
axis(2, seq(0, 6e5, 1e5), as.character(seq(0, 6e2, 1e2)), las = 2)
for (i in 1:7) {
these.pars <- c(rus.nla[1], rus.nla[2] * best.pars[i, 3], best.pars[i, 3], rus.nla[4])
lines(nrow(ds):305, cumsum(mycurve(nrow(ds):305, "logistic", these.pars)) + ds[nrow(ds)-1, "rus"],
lwd = 2, col = mycols[i])
}
these.pars <- c(rus.nla[1], rus.nla[2] * mean(best.pars[, 3]), mean(best.pars[, 3]), rus.nla[4])
lines(nrow(ds):305, cumsum(mycurve(nrow(ds):305, "logistic", these.pars)) + ds[nrow(ds)-1, "rus"],
lwd = 3, lty = 2, col = "black")
legend("topleft", paste0(c(csn[1:7], "Average"), " scenario"),
col = c(mycols[1:7], "black"), lwd = 2, lty = c(rep(1, 7), 2), bty = "n")
dev.off()
mean(best.pars[, 3])
colnames(russia) <- colnames(dcases)[2:5]
row.names(russia) <- c(paste0(csn[1:7], " scenario"),
paste0("Average scenario (s = ", round(mean(best.pars[, 3]), 2), ")"))
stargazer(russia, type = "html", out = "russia-final.html", summary = FALSE)References:
Fernández, C., Steel, M.F.J., 1998. On bayesian modeling of fat tails and skewness. Journal of the American Statistical Association 93, 359–371. [:]