Тест Хаусмана требует эффективности одной из оценок

Тест Хаусмана может быть как полезен, так и вреден в зависимости от обстоятельств, в которых он применяется. Исследователи, использующие тест Хаусмана, должны помнить о том, что его его главное требование — это эффективность одного из методов оценивания, а именно: он должен достигать границы полупараметрической эффективности по Чемберлену (Chamberlain, 1987). Не просто «более точный — менее точный — оба неэффективны», а именно «один должен иметь асимптотически наименьшую дисперсию в классе несмещённых методов оценивания».

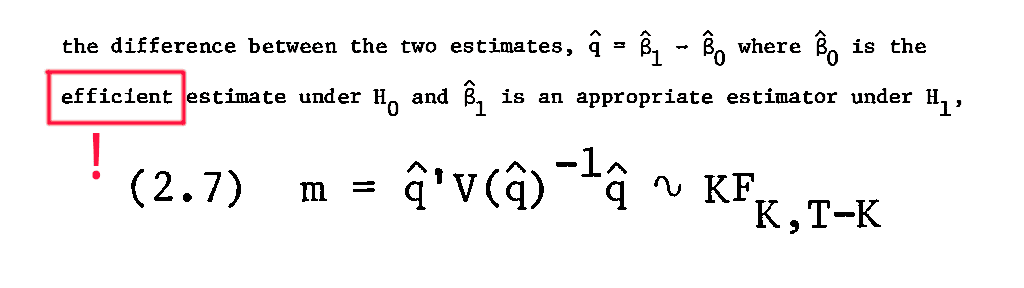
Наблюдение 1. Гетероскедастичность повсюду, это стандарт, данность, непререкаемая реальность, и её надо всегда учитывать (или пользоваться ею).

Наблюдение 2. Предположение об условной гомоскедастичности — старинная чушь, которая рассыпается гнилью на любом наборе реальных данных — даже если какой-то слабенький тестик показывает неотвержение этой гипотезы против какой-то хитровыстроенной узкоспецифичной параметрической альтернативы, — и поэтому как только исследователь начинает опираться на гомоскедастичность, как на костыль, то всё его/её исследование становится инвалидом. Все эти тесты Бройша—Пагана, Глейзера, Уайта и прочие параметрические конструкции — примеры подобных слабых тестов на гомоскедастичность против одной альтернативы (т. е. они не являются омнибус-тестами).

Наблюдение 3. Тесты на условную гомоскедастичность — на равенство неизвестной функции от переменных, сидящих в условии (включённых и исключённых инструментов), константе, — должны непараметрически тестировать совместную значимость группы переменных.

Поэтому легко увидеть, что обычное сравнение «фиксированные или случайные эффекты» (fixed effects vs. random effects) — это фарс: зачем вообще выбирать кривой и потенциально смещённый метод оценки? Только потому, что если в некоторых моделях, оценённых на некоторых наборах данных, оценка случайных эффектов (RE) имеет экономически разумные знаки и магнитуду, в то время как оценка фиксированных эффектов (Within, или FE) обладает бóльшей дисперсией и бóльшим разбросом вокруг нуля или вокруг RE-оценки, не нужно заявлять, что RE-оценка «лучше». Иногда маньяки и преступники бывают любящими отцами.

Оригинальный тест Хаусмана неприменим, когда оба метода оценки неэффективны в своём классе. Преимущество работы с полупараметрически эффективными методами становится очевидным в контексте тестировании пределов по вероятности двух оценок, одна из которых полупараметрически эффективна. В таком случае тест Хаусмана даст корректные результаты вне зависимости от условной дисперсии ошибок модели! Счастливые случаи, в которых этот тест применим, включают следующие методы оценивания:

• Доступный обобщённый метод наименьших квадратов (feasible generalised least squares, FGLS), где условная дисперсия ошибки модели оценивается как функция от всех инструментов непараметрически (например, Robinson (1987) использует веса наблюдений, обратные условной дисперсии);
• Метод решета минимального расстояния (sieve minimum distance, SMD; Ai & Chen (2003));
• Сглаженное эмпирическое правдоподобие (smoothed empirical likelihood, SEL; Kitamura, Tripathi & Ahn (2004));
• Условное евклидово эмпирическое правдоподобие (conditional Euclidean empirical likelihood, C-EEL; Antoine, Bonnal & Renault (2007)).

Случаи, в которых данный тест неприменим без дополнительной корректировки на неэффективность оценки:

• МНК против GMM / 2МНК / IV (ИП) (оба неэффективны из-за гетероскедастичности);
• Фиксированные эффекты против случайных эффектов (конечно же, фиксированные! структура ковариаций ошибок в RE-оценке слишком жёсткая).

Вот краткое доказательство того, почему этот тест работает, когда одна из оценок эффективна и обладает наименьшей дисперсией. Пусть тестируется гипотеза

\[ \mathcal{H}_0\colon \mathop{\mathrm{plim}} \hat\theta_{\mathrm{InEf}} = \mathop{\mathrm{plim}} \hat\theta_{\mathrm{Ef}}\]

против альтернативы \(\mathcal{H}_1\colon \mathcal{H}_0\) неверна. Это эквивалентно тестировнию разницы

\[ \mathop{\mathrm{plim}} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}) = 0\]

Так как \(\hat\theta_{\mathrm{Ef}}\) — вектор, то эту гипотезу можно протестировать с помощью теста Вальда:

\[ \hat W := (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}})' [\mathop{\mathrm{Var}} (\hat\theta_{\mathrm{InEf\mathop{\mathrm{Var}}}} - \hat\theta_{\mathrm{Ef}})]^{-1} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}),\]

где дисперсия в середине — это асимптотическая дисперсия, делённая на n.

Утверждение. Если \(\hat\theta_{\mathrm{InEf}}\) состоятельна и \(\hat\theta_{\mathrm{Ef}}\) состоятельная и эффективна, то тогда

\[ \mathop{\mathrm{Var}} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}) = \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}.\]

Доказательство. Пусть \(\alpha \in \mathbb{R}\) — любое действительное число. Пусть оно определяет линейную комбинацию двух оценок:

\[ \mathop{\mathrm{Var}} \hat\theta_{\alpha} := \alpha \hat\theta_{\mathrm{InEf}} + (1-\alpha) \hat\theta_{\mathrm{Ef}}.\]

Её дисперсия — это функция от \(\alpha\):

\[ V(\alpha) := \mathop{\mathrm{Var}} \hat\theta_\alpha = \alpha^2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} + (1-\alpha)^2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} + 2 \alpha (1- \alpha) \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}).\]

Так как эта линейная комбинация даёт эффективную оценку при \(\alpha = 0\), то \(V(0) \ge \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}\). Иными словами, \(\forall \alpha \in \mathbb{R}\), \(V(\alpha) \ge V(0)\). Это значит, что ноль — это локальный оптимум V: \(V'(0) = 0\). Из этого следует

\[ V'(\alpha) = 2\alpha \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - 2(1-\alpha) \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}} + (2-4\alpha) \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}).\]

Подстановка \(\alpha = 0\) даёт

\[ V'(0) = -2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}} + 2 \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}) = 0,\]

но так как \(V'(0) = 0\), то

\[ \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}) = \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}.\]

Это даёт искомую статистику теста Хаусмана

\[ \hat W := (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}})' [\mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - \mathop{\mathrm{Var}}\hat\theta_{\mathrm{Ef}}]^{-1} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}),\]

которая имеет распределение \(\chi^2_{\dim\hat\theta_{\mathrm{Ef}}}\) при нулевой гипотезе и стандартных предпосылках.