z--- title: "The Hausman test requires one estimator to be efficient" date: "2025-05-26" published: true

The Hausman test requires one estimator to be efficient

The Hausman test is useful in many circumstances but harmful in many common situation. Researchers using the Hausman test must not forget that its main assumption is the efficiency of one of the estimators: it must attain the semi-parametric efficiency bound in the sense of Chamberlain (1987). Not just ‘more accurate’ -- but just ‘efficient’, i.e. having the lowest variance in the appropriate family of unbiased estimators.

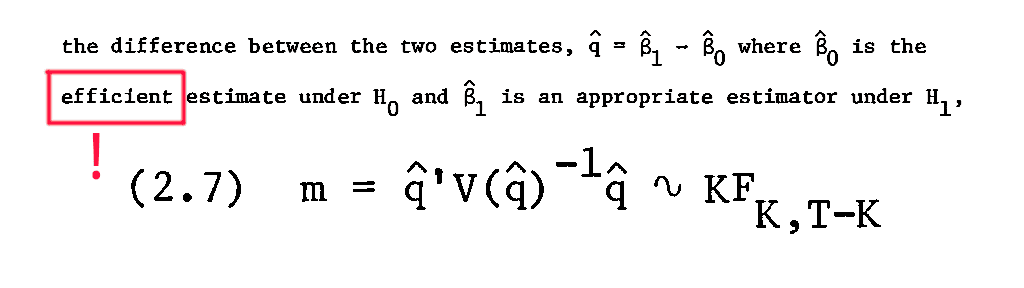
Observation 1. Heteroskedasticity is everywhere, it is the standard, it is undeniable, and it must be taken into account in some way or form.

Observation 2. The assumption of conditional homoskedasticity is rotten, never holds in real-world data sets – even is one's tests do not reject the null against one highly specific and implausibly parametric specification – and therefore invalidates one's research findings the moment it is assumed. Breusch--Pagan, Glejser, White, and other tests for homoskedasticity are examples of such specific parametric alternatives (i.e. they are not omnibus).

Observation 3. Testing for conditional homoskedasticity – constancy of an unknown function with respect to the conditioning variables, i.e. included and excluded instruments – requires non-parametric methods for testing joint significance of a group of variables.

It is easy to see why the usual comparison ‘fixed effects vs. random effects’ is a joke: why would one prefer a wrong and potentially biased estimator? Just because in certain models estimated on certain data sets, the random-effects (RE) estimator has significant coefficients with economically meaningful signs, and the fixed-effects (FE) estimator has a higher variance and point estimates with a wider dispersion around zero / RE values, it does not mean that the RE estimator is better. Sometimes, serial killers and mass murderers can be loving parents, too.

The original version of the Hausman test is not applicable when both estimators are not efficient. The benefit of working with semi-parametrically efficient estimators becomes obvious in the context of testing the equality of probability limits of two estimators, one of which is semi-parametrically efficient. Then, the Hausman test produces correct results regardless of the conditional variance of the model error! Cases where this test is applicable may involve the following efficient estimators:

• Feasible generalised least squares (FGLS) where the conditional variance of the model error given the instruments is modelled non-parametrically (e.g. Robinson (1987) inverse-variance-weighted estimator);
• Sieve minimum distance (SMD) of Ai & Chen (2003);
• Smoothed empirical likelihoiod (SEL) of Kitamura, Tripathi & Ahn (2004);
• Conditional Euclidean empirical likelihood (C-EEL) of Antoine, Bonnal & Renault (2007).

Cases where this test is still not applicable without further correction include:

• OLS vs GMM / 2SLS / IV (neither is efficient due to heteroskedastic errors);
• Fixed effects vs. random effects (of course, fixed effects! the parametric structure of the RE estimator is too strong an assumption).

Here is a short proof that relies on the fact that one of the estimators must be fully efficient. Consider testing the hypothesis

\[ \mathcal{H}_0\colon \mathop{\mathrm{plim}} \hat\theta_{\mathrm{InEf}} = \mathop{\mathrm{plim}} \hat\theta_{\mathrm{Ef}}\]

versus the alternative \(\mathcal{H}_1\colon \mathcal{H}_0\) is not true. This is equivalent to testing

\[ \mathop{\mathrm{plim}} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}) = 0\]

Since \(\hat\theta_{\mathrm{Ef}}\) is a vector, this hypothesis can be tested using the Wald test:

\[ \hat W := (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}})' [\mathop{\mathrm{Var}} (\hat\theta_{\mathrm{InEf\mathop{\mathrm{Var}}}} - \hat\theta_{\mathrm{Ef}})]^{-1} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}),\]

where the variance in the middle is the asymptotic variance divided by n.

Claim. If \(\hat\theta_{\mathrm{InEf}}\) is consistent and \(\hat\theta_{\mathrm{Ef}}\) is consistent and efficient, then

\[ \mathop{\mathrm{Var}} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}) = \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}.\]

Proof. Let \(\alpha \in \mathbb{R}\) be any real number that defines a linear combination of the two estimators: [\mathop{\mathrm{Var}} \hat\theta{\alpha} := \alpha \hat\theta{\mathrm{InEf}} + (1-\alpha) \hat\theta_{\mathrm{Ef}}. ] Its variance is a function of \(\alpha\):

\[ V(\alpha) := \mathop{\mathrm{Var}} \hat\theta_\alpha = \alpha^2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} + (1-\alpha)^2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} + 2 \alpha (1- \alpha) \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}).\]

Since this linear combination yield an efficient estimator at \(\alpha = 0\), it follows that \(V(0) \ge \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}\). In other words, \(\forall \alpha \in \mathbb{R}\), \(V(\alpha) \ge V(0)\). This implies that zero is a local optimum of V: \(V'(0) = 0\). This implies

\[ V'(\alpha) = 2\alpha \mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - 2(1-\alpha) \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}} + (2-4\alpha) \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}).\]

Plugging \(\alpha = 0\) yields

\[ V'(0) = -2 \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}} + 2 \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}) = 0,\]

but since \(V'(0) = 0\), it follows that

\[ \mathop{\mathrm{Cov}} (\hat\theta_{\mathrm{InEf}}, \hat\theta_{\mathrm{Ef}}) = \mathop{\mathrm{Var}} \hat\theta_{\mathrm{Ef}}.\]

This yields the sought-after Hausman statistic

\[ \hat W := (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}})' [\mathop{\mathrm{Var}} \hat\theta_{\mathrm{InEf}} - \mathop{\mathrm{Var}}\hat\theta_{\mathrm{Ef}}]^{-1} (\hat\theta_{\mathrm{InEf}} - \hat\theta_{\mathrm{Ef}}),\]

that is distributed as \(\chi^2_{\dim\hat\theta_{\mathrm{Ef}}}\) under the hull hypothesis and standard assumptions.