Отличная задачка для тех, кто любит боль.
Задача. Агафья Степанна стала ипохондриком и теперь очень боится заболеть — она каждый час измеряет свою температуру градусником. Она бывает больше либо равной 36,6° (т. е. 36,6° плюс «надбавка».), причём «надбавка» распределена экспоненциально с параметром \(\lambda=4\). Если результат измерения превысил 37°, то Степанна начинает волноваться и оттого температурит так, что каждый следующий час результат измерения увеличивается по сравнению с предыдущим на случайную величину, имеющую то же самое распределение, что и надбавка (\(\mathop{\mathrm{Exp}}(4)\)). Как только достигнут или превышен потолок в 40°, Степанна теряет сознание, холодеет, и через час её температура возвращается на отметку 36,6°, а сама Степанна приходит в сознание и радуется тому, что абсолютно здорова. После этого она снова каждый час мерит температуру по тому же принципу.
- Каково математическое ожидание её температуры за всё время?
- Какой процент всего времени Степанна температурит (\(t\geqslant37^{\circ}\))? Какова средняя продолжительность её здорового состояния? Какова средняя продолжительность её болезни? (Длина блуждания.)
- Если ипохондрик потеряла сознание, то какова вероятность, что она увидела на градуснике отметку выше, чем 40,5°? (Условная вероятность.)
- Новое условие: предположим, что если температура подскакивает до 41° или выше, то старушка умирает. (Это вполне возможное событие: если было 39,9°, а потом раз — и резко подскочила на 1,15° или выше; вероятность скачка на 1,15° или более равна ≈0,01.) Сколько часов в среднем живут старушки с того момента, как становятся ипохондриками? Каково матожидание температуры живых старушек? Если температура в пределах нормы, то какова вероятность умереть при следующем взлёте температуры? А в один из десяти следующих взлётов? (Длина блуждания. Теперь из матожидания будут выброшены аутлайеры, оно чуть понизится, но совсем на кроху.)
- Как изменятся все ответы в предыдущих пунктах, если после потери сознания старушкина температура падает не до 36,6°, а до 36,6° плюс надбавка (т. е. сразу разыгрывается случайным образом)?
Я боль не очень люблю, поэтому приведу не решение, а собственные размышления на тему.
Мне кажется, имеет смысл рассмотреть такой случайный процесс: есть нижняя граница коридора (36,6), средняя (37), верхняя (40) и смертельная (41). В коридоре в каждый момент времени с пола подпрыгивает частица. Как только в момент времени величина выскакивает из средней границы коридора, то начинается случайное блуждание вверх. Как только в результате случайного однонаправленного блуждания частица пробивает потолок, то частица падает на пол, и снова начинаются случайные прыжки с пола. Если же, вылетая, частица пересекла смертельную границу, то игра заканчивается. Требуется найти среднюю вертикальную координату этой частицы, а также долю наблюдений, когда частица вне меньшего коридора... Вроде всё понятно. Кстати, процент времени болезни не может быть равен 100, так как после каждого «рекорда» следующий период она здорова (36,6), а длина температуренья конечна (кстати, это потребуется доказать в процессе решения).
Реализация Агафьи Степанны в пакете Mathematica.
t = 1; (\* Начальный момент времени... 1 или 0 на вкус\*)
x = 36.6; (\* Пол \*)
i = 1; (\* Для того чтобы делать циклы \*)
cycles = 10000; (\* Как бы количество циклов \*)
coord = { }; (\* Резервируем место под запись наблюдений \*)
While\[i < cycles, (\* Главный цикл \*)
x += RandomVariate\[ExponentialDistribution\[4\]\]; (\* Разыгрываем прыжок темп. с пола \*)
If\[ (\* НАЧАЛО ЕСЛИ \*)
x < 37, (\* ЕСЛИ не выскочили, то \*)
AppendTo\[coord, {t, x}\]; (\* ТОГДА Пишем в хронику номер наблюдения и темп., \*)
x = 36.6; t++, (\* Обнуляем частицу, разыгрываем следующее наблюдение \*)
While\[x < 40, (\* ИНАЧЕ ЦИКЛ2: будем расти, пока меньше 40 \*)
AppendTo\[coord, {t, x}\]; (\* Пишем в хронику номер наблюдения и темп., \*)
x += RandomVariate\[ExponentialDistribution\[4\]\]; (\* Снова растём, ибо больны \*)
t++ (\* Разыгрываем следующее наблюдение \*)
\]; (\*КОНЕЦ ЦИКЛ2, когда стало выше 40 \*)
AppendTo\[coord, {t, x}\]; (\* Пишем точку, которая выше 40 \*)
t++; (\* Ждём 1 час, пока без сознания \*)
x = 36.6; (\* Охлаждаем тело \*)
AppendTo\[coord, {t, x}\]; (\* Записываем здоровое наблюдение \*)
(\* Закомментировать предыдущую строку для последнего пункта задачи \*)
t++; (\* Разыгрываем следующее наблюдение \*)
(\* Закомментировать предыдущую строку для последнего пункта задачи \*)
\]; (\* КОНЕЦ ЕСЛИ
i++ (\* Перейти к следующей процедуре проверки
\]; (\* Конец главного цикла
(\*Print\[TraditionalForm\[coord\]\];\*)
(\* Предыдущая строка, если снять комментарий, выводит таблицу наблюдений \*)
(\* Я по ней проверял, не потерялось ли чего \*)
(\* А теперь рисуем все наблюдения \*)
Show\[
ListPlot\[coord, PlotStyle -> Directive\[PointSize\[Medium\], Black\], (\* Наблюдения чёрными точками \*)
PlotRange -> All\],
ListLinePlot\[{{0, 37}, {t, 37}}, (\* Горизонтальные линии пороговых уровней \*)
PlotStyle -> {Thickness\[0.002\], Red, Dashed}\],
ListLinePlot\[{{0, 40}, {t, 40}},
PlotStyle -> {Thickness\[0.002\], Red, Dashed}\],
ListLinePlot\[{{0, 41}, {t, 41}},
PlotStyle -> {Thickness\[0.002\], Red, Dashed}\]
\]20 наблюдений: 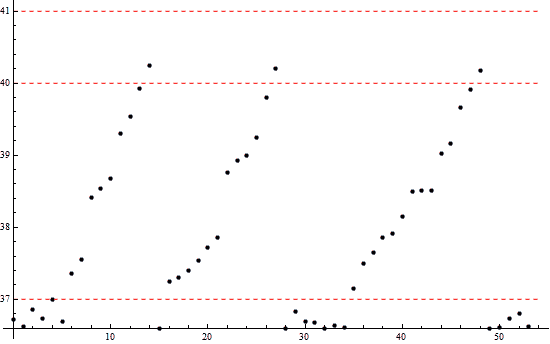
200 наблюдений: 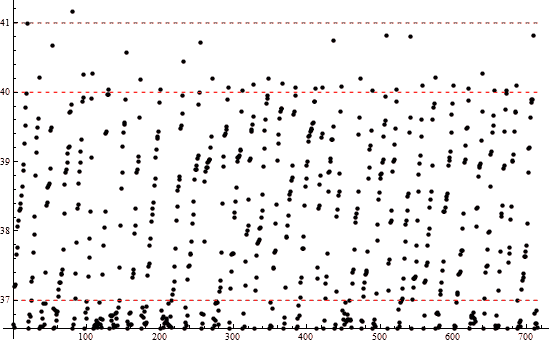
2 000 наблюдений: 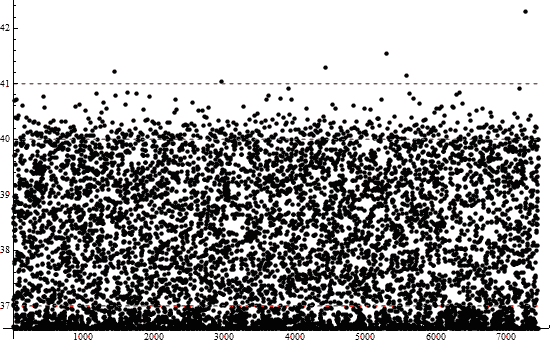
20 000 наблюдений: 
По увидении этих картинок можно прийти к выводу (правда, это надо ещё и обосновать), что если температура подскочит выше 42°, то старушка взрывается... шутка! Можно прийти к выводу, что если принять условие пункта 4, то дни старушки сочтены, длина жизни конечна; ведь так много серьёзных прыжков...
Особенность программы: количество циклов становится количеством наблюдений, когда частица в коридоре. В итоге реально всего шагов в симуляторе становится не столько, сколько циклов, а примерно в 3,3 раза больше. Можно было бы реализовать так, чтобы сколько задали, столько и было, но это нужно подумать и что-то основное поменять (наложить проверку не на номер цикла, на t).
P.S. MathJax поддерживает знаки нестрогого неравенства с наклонными чёрточками, кои так характерны для русской типографики: \leqslant и \geqslant. Не забудьте включить AMS в конфигурации MathJax, и будет вам счастье: \(\leqslant\), \(\geqslant\).